Trong bài toán này, chúng ta được đưa ra một cây có kích thước N, một nút của cây V và k. Nhiệm vụ của chúng ta là tìm nút thứ K trong đường truyền DFS của một cây con đã cho trong Cây .
Chúng ta cần tìm nút thứ k trong đường truyền DFS của cây bắt đầu từ đỉnh V.
Hãy lấy một ví dụ để hiểu vấn đề,
Đầu vào:
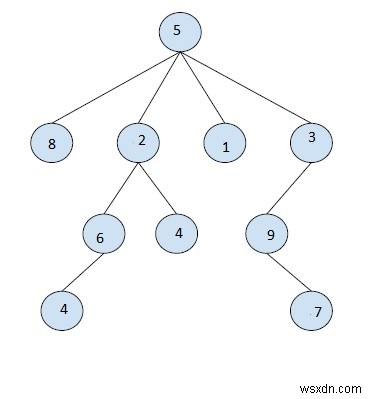
V =2, k =3
Đầu ra:4
Giải thích -
Chuỗi là {1, 2, 3, 5, 6, 7} Phần tử thứ 4 là 5. Phương pháp tiếp cận giải pháp
Một giải pháp đơn giản cho vấn đề là tìm đường truyền DFS của nút V và in giá trị thứ k từ nút này.
Đối với điều này, chúng tôi thực hiện duyệt DFS của cây và lưu trữ nó trong một vectơ. Trong vectơ này, chúng tôi sẽ tìm các giá trị cho V start và V end đánh dấu điểm bắt đầu và kết thúc của quá trình truyền DFS của cây. Sau đó, tìm giá trị thứ k trong phạm vi này và in nó nếu có thể.
Ví dụ
Chương trình minh họa hoạt động của giải pháp của chúng tôi
#includeusing namespace std; #define N 100005int n; vector tree [N]; int currentIdx; vector startIdx, endIdx; vector dfsTraversalVector; void insertEdge (int u, int v) {tree [u] .push_back (v); tree [v] .push_back (u);} void findDfsTraversal (int ch, int par) {dfsTraversalVector [currentIdx] =ch; startIdx [ch] =currentIdx ++; for (auto c:tree [ch]) {if (c! =par) findDfsTraversal (c, ch); } endIdx [ch] =currentIdx - 1;} int findKNodeDfsV (int v, int k) {k =k + (startIdx [v] - 1); if (k <=endIdx [v]) trả về dfsTraversalVector [k]; return -1;} int main () {n =9; insertEdge (5, 8); insertEdge (5, 2); insertEdge (5, 10); insertEdge (5, 3); insertEdge (2, 6); insertEdge (2, 1); insertEdge (3, 9); insertEdge (6, 1); insertEdge (9, 7); startIdx.resize (n); endIdx.resize (n); dfsTraversalVector.resize (n); findDfsTraversal (5, 0); int v =2, k =4; cout < Đầu ra
Nút thứ 4 trong DFS của nút 2 là 1
