Khái niệm
Bài viết giải thích một phương pháp giải bài toán tìm LCA của hai nút trong một cây bằng cách rút gọn nó thành bài toán RMQ.
Ví dụ
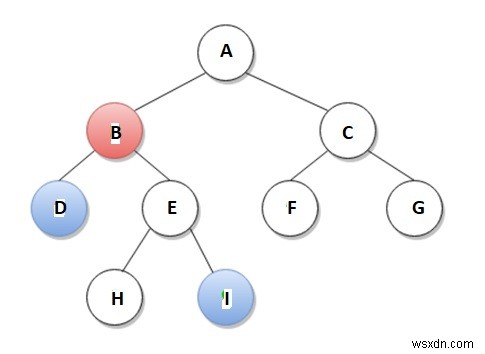
Tổ tiên chung thấp nhất (LCA) của hai nút a và b trong cây gốc T được định nghĩa là nút nằm xa gốc nhất có cả a và b là con cháu.
Ví dụ, theo sơ đồ dưới đây, LCA của nút D và nút I là nút B.
Chúng ta có thể áp dụng nhiều cách tiếp cận để giải quyết vấn đề LCA. Các cách tiếp cận này khác nhau tùy theo sự phức tạp về thời gian và không gian của chúng.
Truy vấn tối thiểu phạm vi (RMQ) được áp dụng trên mảng để xác định vị trí của phần tử có giá trị nhỏ nhất giữa hai chỉ số được chỉ định. Chúng ta có thể áp dụng các cách tiếp cận khác nhau để giải RMQ. Theo bài viết này, cách tiếp cận dựa trên Cây phân đoạn được giải thích. Đối với cây phân đoạn, thời gian tiền xử lý là O (n) và thời gian để truy vấn phạm vi tối thiểu là O (Logn). Ở đây, không gian bổ sung cần thiết là O (n) để lưu trữ cây phân đoạn.
Giảm LCA xuống RMQ
Chúng tôi giải thích ý tưởng này để thăm cây bắt đầu từ gốc bằng chuyến tham quan Euler (Ghé thăm mà không cần nhấc bút chì), là kiểu truyền tải kiểu DFS (Tìm kiếm đầu tiên) với các đặc điểm truyền tải đặt trước.
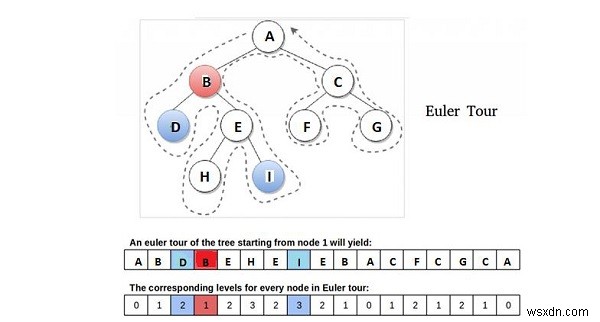
Quan sát - Theo sơ đồ trên, LCA của nút D và I là nút B, cho biết là nút gần gốc nhất trong số tất cả những gì gặp phải giữa các lần truy cập của D và I trong DFS của T. Vì vậy, chúng ta có thể nói quan sát này là chìa khóa để giảm. Một lần nữa, chúng ta có thể nói rằng nút của chúng ta là nút ở mức tối thiểu và là nút duy nhất ở mức đó trong số tất cả các nút xuất hiện giữa các lần xuất hiện liên tiếp (bất kỳ) của a và b trong chuyến tham quan Euler của T.
Chúng tôi yêu cầu ba mảng để triển khai -
-
Các nút đã ghé thăm theo thứ tự chuyến tham quan Euler của T
-
Mỗi Cấp độ nút đã truy cập trong chuyến tham quan Euler của T
-
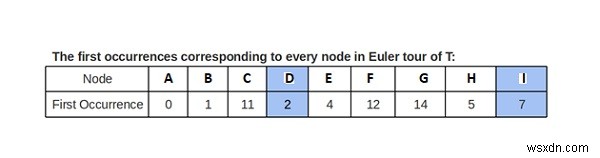
Chỉ số lần xuất hiện đầu tiên của Node trong chuyến tham quan Euler của T (vì bất kỳ lần xuất hiện nào đều tốt, hãy theo dõi chỉ số đầu tiên)
Phương pháp
-
Thực hiện chuyến tham quan Euler trên cây và điền vào các mảng euler, cấp và lần xuất hiện đầu tiên.
-
Áp dụng mảng xuất hiện đầu tiên, lấy các chỉ số tương ứng với hai nút sẽ là các góc của phạm vi trong mảng mức được cung cấp cho thuật toán RMQ để có giá trị nhỏ nhất.
-
Tại thời điểm thuật toán trả về chỉ số của mức tối thiểu trong phạm vi, chúng tôi áp dụng nó để xác định LCA bằng cách sử dụng mảng tham quan Euler.
Ví dụ
/* This C++ Program is implemented to find LCA of u and v by reducing the problem to RMQ */
#include<bits/stdc++.h>
#define V 9 // indicates number of nodes in input tree
int euler1[2*V - 1]; // indicates for Euler tour sequence
int level1[2*V - 1]; // indicates level of nodes in tour sequence
int firstOccurrence1[V+1]; // indicates first occurrences of nodes in tour
int ind; // indicates variable to fill-in euler and level arrays
//This is a Binary Tree node
struct Node1{
int key;
struct Node1 *left, *right;
};
// Utility function creates a new binary tree node with given key
Node1 * newNode1(int k){
Node1 *temp = new Node1;
temp->key = k;
temp->left = temp->right = NULL;
return temp;
}
// indicates log base 2 of x
int Log2(int x){
int ans = 0 ;
while (x>>=1) ans++;
return ans ;
}
/* A recursive function is used to get the minimum value in a given range of array indexes. The following are parameters for this function.
st --> indicates pointer to segment tree
index --> indicates index of current node in the segment tree.
Initially 0 is passed as root is always at index 0
ss & se --> indicate starting and ending indexes of the segment
represented by current node, i.e., st[index]
qs & qe --> indicate starting and ending indexes of query range
*/
int RMQUtil(int index1, int ss1, int se1, int qs1, int qe1, int *st1){
// It has been seen that if segment of this node is a part of given range, then return the min of the segment
if (qs1 <= ss1 && qe1 >= se1)
return st1[index1];
//It has been seen that if segment of this node is outside the given range
else if (se1 < qs1 || ss1 > qe1)
return -1;
// It has been seen that if a part of this segment overlaps with the given range
int mid = (ss1 + se1)/2;
int q1 = RMQUtil(2*index1+1, ss1, mid, qs1, qe1, st1);
int q2 = RMQUtil(2*index1+2, mid+1, se1, qs1, qe1, st1);
if (q1==-1) return q2;
else if (q2==-1) return q1;
return (level1[q1] < level1[q2]) ? q1 : q2;
}
// Return minimum of elements in range from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
int RMQ(int *st1, int n, int qs1, int qe1){
// Check for erroneous input values
if (qs1 < 0 || qe1 > n-1 || qs1 > qe1){
printf("Invalid Input");
return -1;
}
return RMQUtil(0, 0, n-1, qs1, qe1, st1);
}
// Now a recursive function that constructs Segment Tree for
array[ss1..se1]. // si1 is index of current node in segment tree st
void constructSTUtil(int si1, int ss1, int se1, int arr1[], int *st1){
// When there will be only one element in array, store it in current node of
// segment tree and return
if (ss1 == se1)st1[si1] = ss1;
else{
// It has been seen that if there are more than one
elements, then recur for left and right subtrees and store the
minimum of two values in this node
int mid1 = (ss1 + se1)/2;
constructSTUtil(si1*2+1, ss1, mid1, arr1, st1);
constructSTUtil(si1*2+2, mid1+1, se1, arr1, st1);
if (arr1[st1[2*si1+1]] < arr1[st1[2*si1+2]])
st1[si1] = st1[2*si1+1];
else
st1[si1] = st1[2*si1+2];
}
}
/* Now this function is used to construct segment tree from given
array. This function allocates memory for segment tree and calls
constructSTUtil() to fill the allocated memory */
int *constructST(int arr1[], int n){
// Allocating memory for segment tree
//Indicates height of segment tree
int x = Log2(n)+1;
// Indicates maximum size of segment tree
int max_size = 2*(1<<x) - 1; // 2*pow(2,x) -1
int *st1 = new int[max_size];
// Indicates filling the allocated memory st1
constructSTUtil(0, 0, n-1, arr1, st1);
// Returning the constructed segment tree
return st1;
}
// Indicates recursive version of the Euler tour of T
void eulerTour(Node1 *root, int l){
/* if the passed node exists */
if (root){
euler1[ind] = root->key; // inserting in euler array
level1[ind] = l; // inserting l in level array
ind++; // indicates increment index
/* It has been seen that if unvisited, mark first occurrence*/
if (firstOccurrence1[root->key] == -1)
firstOccurrence1[root->key] = ind-1;
/* touring left subtree if exists, and remark euler
and level arrays for parent on return */
if (root->left){
eulerTour(root->left, l+1);
euler1[ind]=root->key;
level1[ind] = l;
ind++;
}
/* touring right subtree if exists, and remark euler
and level arrays for parent on return */
if (root->right) {
eulerTour(root->right, l+1);
euler1[ind]=root->key;
level1[ind] = l;
ind++;
}
}
}
// Returning LCA of nodes n1, n2 (assuming they are
// present in the tree)
int findLCA(Node1 *root, int u1, int v1){
/* Marking all nodes unvisited. Note that the size of
firstOccurrence is 1 as node values which vary from
1 to 9 are used as indexes */
memset(firstOccurrence1, -1, sizeof(int)*(V+1));
/* To start filling euler and level arrays from index 0 */
ind = 0;
/* Starting Euler tour with root node on level 0 */
eulerTour(root, 0);
/* constructing segment tree on level array */
int *st1 = constructST(level1, 2*V-1);
/*It has been seen that if v before u in Euler tour. For RMQ to
work, first parameter 'u1' must be smaller than second 'v1' */
if (firstOccurrence1[u1]>firstOccurrence1[v1])
std::swap(u1, v1);
// Indicates starting and ending indexes of query range
int qs1 = firstOccurrence1[u1];
int qe1 = firstOccurrence1[v1];
// Indicates query for index of LCA in tour
int index1 = RMQ(st1, 2*V-1, qs1, qe1);
/* returning LCA node */
return euler1[index1];
}
// Driver program to test above functions
int main(){
// Let us create the Binary Tree as shown in the diagram.
Node1 * root = newNode1(1);
root->left = newNode1(2);
root->right = newNode1(3);
root->left->left = newNode1(4);
root->left->right = newNode1(5);
root->right->left = newNode1(6);
root->right->right = newNode1(7);
root->left->right->left = newNode1(8);
root->left->right->right = newNode1(9);
int u1 = 4, v1 = 9;
printf("The LCA of node %d and node %d is node %d.\n",
u1, v1, findLCA(root, u1, v1));
return 0;
} Đầu ra
The LCA of node 4 and node 9 is node 2.
