Chương trình C ++ để tìm ra số lượng ô cần chặn trong lưới để tạo đường dẫn

Giả sử, có một lưới kích thước h * w. Có một robot ở vị trí ô (0, 0) và nó phải đi đến vị trí (h - 1, w - 1). Có hai loại ô trong lưới, bị chặn và không bị chặn. Robot có thể đi qua các ô không bị chặn nhưng không thể đi qua các ô bị chặn. Robot có thể đi bốn hướng; nó có thể đi sang trái, phải, lên và xuống. Nhưng rô bốt có thể đi theo bất kỳ hướng nào từ ô này sang ô khác (bỏ qua ô trước đó mà nó nằm trong đó), vì vậy chúng ta chỉ phải tạo một con đường và chặn tất cả các ô khác không nằm trong con đường đó. Chúng ta phải tìm ra và trả về bao nhiêu ô chúng ta phải chặn để tạo một đường dẫn cho robot từ (0, 0) đến (h - 1, w - 1) và nếu không có đường đi nào có thể, chúng ta trả về -1.

Vì vậy, nếu đầu vào là h =4, w =4, grid ={".. #.", "#. #.", "#. ##", "# ..."}, thì đầu ra sẽ là 2.

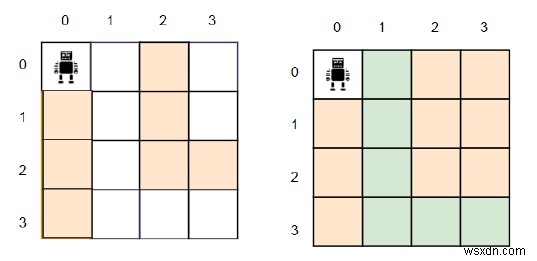
Chúng tôi chỉ phải chặn hai ô để tạo một đường dẫn duy nhất từ ​​(0, 0) đến (3, 3).

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

Define one 2D array dp
dp[0, 0] := 0
Define an array moves containing pairs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
Define one queue q
insert pair (0, 0) at the end of q
while (not q is empty), do:
   p := first element of q
   delete first element from q
   for initialize i := 0, when i < 4, update (increase i by 1), do:
      row := first value of p + first value of moves[i]
      col := second value of p + second value of moves[i]
      if row < 0 or row > h - 1 or col < 0 or col > w - 1, then:
         Ignore following part, skip to the next iteration
      if grid[row, col] is same as '#', then:
         Ignore following part, skip to the next iteration
      if dp[first value of p, second value of p] + 1 < dp[row, col], then:
         dp[row, col] := dp[first value of p, second value of p] + 1
         insert pair(row, col) into q
if dp[h - 1, w - 1] is same as 2500, then:
   return -1
count := 0
   for initialize i := 0, when i < h, update (increase i by 1), do:
      for initialize j := 0, when j < w, update (increase j by 1), do:
      if grid[i, j] is same as '.', then:
         (increase count by 1)
return count - (dp[h - 1, w - 1] + 1)

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;

int solve(int h, int w, vector<string> grid){
   vector<vector<int>> dp(h, vector<int>(w, 2500));
   dp[0][0] = 0;
   vector<pair<int, int>> moves = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
   queue<pair<int, int>> q;
   q.push(make_pair(0, 0));
   while (!q.empty()) {
      auto p = q.front();
      q.pop();
      for (int i = 0; i < 4; i++) {
         int row = p.first + moves[i].first;
         int col = p.second + moves[i].second;
         if (row < 0 || row > h - 1 || col < 0 || col > w - 1) continue;
         if (grid[row][col] == '#') 
            continue;
         if (dp[p.first][p.second] + 1 < dp[row][col]) {
            dp[row][col] = dp[p.first][p.second] + 1; q.push(make_pair(row, col));
         }
      }
   }
   if (dp[h - 1][w - 1] == 2500) {
      return -1;
   }
   int count = 0;
   for (int i = 0; i < h; i++) {
      for (int j = 0; j < w; j++) {
         if (grid[i][j] == '.') count++;
      }
   }
   return count - (dp[h - 1][w - 1] + 1);
}
int main() {
   int h = 4, w = 4;
   vector<string> grid = {"..#.", "#.#.", "#.##", "#..."};
   cout<< solve(h, w, grid);
   return 0;
}

Đầu vào

4, 4, {"..#.", "#.#.", "#.##", "#..."}

Đầu ra

2