Chương trình C ++ để tìm ra số điểm tối đa có thể giảm từ một biểu đồ

Giả sử, có một đồ thị có trọng số, vô hướng có n đỉnh và m cạnh. Điểm của đồ thị được định nghĩa là phép cộng của tất cả các trọng số các cạnh trong đồ thị. Trọng số của các cạnh có thể là số âm, và nếu chúng bị loại bỏ thì điểm của đồ thị sẽ tăng lên. Những gì chúng ta phải làm, chúng ta phải làm cho điểm của đồ thị nhỏ nhất bằng cách loại bỏ các cạnh khỏi đồ thị trong khi vẫn giữ cho đồ thị liên thông. Chúng tôi phải tìm ra số điểm tối đa có thể bị giảm.

Biểu đồ được cho trong một mảng 'các cạnh', trong đó mỗi phần tử có dạng {weight, {vertex1, vertex2}}.

Vì vậy, nếu đầu vào là n =5, m =6, các cạnh ={{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3 , {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}, thì đầu ra sẽ là 4.

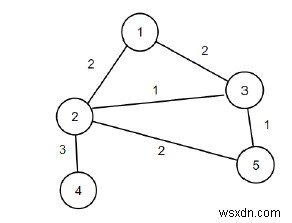
Nếu chúng ta xóa cạnh (1, 2) và (2, 5) khỏi biểu đồ, tổng số điểm giảm sẽ là 4 và biểu đồ sẽ vẫn được kết nối.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau−

cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
   par[v] := v
   dim[v] := 1
Define a function find(), this will take v,
   if par[v] is same as v, then:
      return v
   return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
   (decrease cnum by 1)
   if dim[a] > dim[b], then:
      swap values of (a, b)
   par[a] := b
   dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
   make(i)
res := 0
for each edge in edges, do:
   a := first vertex of edge
   b := second vertex of edge
   weight := weight of edge
   if find(a) is same as find(b), then:
      if weight >= 0, then:
         res := res + 1 * weight
      Ignore following part, skip to the next iteration
   if cnum is same as 1, then:
      if weight >= 0, then:
         res := res + 1 * weight
   Otherwise
      unify(a, b)
return res

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;

int cnum = 0;
int par[100];
int dim[100];

void make(int v){
   par[v] = v;
   dim[v] = 1;
}
int find(int v){
   if(par[v] == v)
   return v;
   return par[v] = find(par[v]);
}
void unify(int a, int b){
   a = find(a); b = find(b);
   if(a != b){
      cnum--; if(dim[a] > dim[b]){
         swap(a, b);
      }
      par[a] = b; dim[b] += dim[a];
   }
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
   cnum = n;
   sort(edges.begin(), edges.end());
   for(int i = 1; i <= n; i++)
      make(i);
   int res = 0;
   for(auto &edge : edges){
      int a = edge.second.first;
      int b = edge.second.second;
      int weight = edge.first;
      if(find(a) == find(b)) {
         if(weight >= 0) 
            res += 1 * weight;
         continue;
      }
      if(cnum == 1){
         if(weight >= 0)
            res += 1 * weight;
      } else{
         unify(a, b);
      }
   }
   return res;
}
int main() {
   int n = 5, m = 6;
   vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
   cout<< solve(n, m, edges);
   return 0;
}

Đầu vào

5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}

Chương trình C ++ để tìm ra số điểm tối đa có thể giảm từ một biểu đồ

Ví dụ

Đầu vào

Đầu ra