Chương trình Python để phát hiện chu kỳ trong đồ thị được hướng dẫn

Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu hỏi được đưa ra bên dưới.

Tuyên bố sự cố - Ta được đồ thị có hướng, ta cần kiểm tra xem đồ thị có chứa chu trình hay không. Kết quả đầu ra phải đúng nếu đồ thị đã cho chứa ít nhất một chu kỳ, ngược lại là sai.

Bây giờ chúng ta hãy quan sát giải pháp trong việc triển khai bên dưới -

Ví dụ

# collections module
from collections import defaultdict
# class for creation of graphs
class Graph():
   # constructor
   def __init__(self, vertices):
      self.graph = defaultdict(list)
      self.V = vertices
   def addEdge(self, u, v):
      self.graph[u].append(v)
   def isCyclicUtil(self, v, visited, recStack):
      # Marking current node visited and addition to recursion stack
      visited[v] = True
      recStack[v] = True
      # if any neighbour is visited and in recStack then graph is cyclic in nature
      for neighbour in self.graph[v]:
         if visited[neighbour] == False:
            if self.isCyclicUtil(neighbour, visited, recStack) == True:
               return True
         elif recStack[neighbour] == True:
            return True
      # pop the node after the end of recursion
      recStack[v] = False
      return False
   # Returns true if graph is cyclic
   def isCyclic(self):
      visited = [False] * self.V
      recStack = [False] * self.V
      for node in range(self.V):
         if visited[node] == False:
            if self.isCyclicUtil(node, visited, recStack) == True:
               return True
      return False
g = Graph(4)
g.addEdge(0, 3)
g.addEdge(0, 2)
g.addEdge(3, 2)
g.addEdge(2, 0)
g.addEdge(1, 3)
g.addEdge(2, 1)
if g.isCyclic() == 1:
   print ("Graph is cyclic in nature")
else:
   print ("Graph is non-cyclic in nature")

Đầu ra

Graph is cyclic in nature

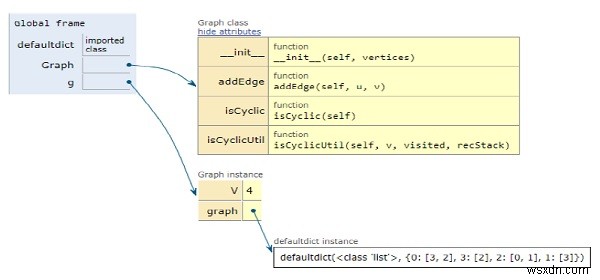
Tất cả các biến được khai báo trong phạm vi cục bộ và các tham chiếu của chúng được hiển thị trong hình trên.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về cách chúng ta có thể tạo Chương trình Python để phát hiện chu kỳ trong đồ thị được hướng dẫn