Tìm xem có một đường dẫn dài hơn k từ một nguồn trong Python hay không

Giả sử chúng ta có một đồ thị, chúng ta cũng có một đỉnh nguồn và một số k. K là độ dài đường đi của đồ thị giữa nguồn đến đích, chúng ta phải kiểm tra xem liệu chúng ta có thể tìm thấy một đường đơn giản (không có chu trình) bắt đầu từ nguồn và kết thúc tại bất kỳ đỉnh nào khác (là đích) hay không. Biểu đồ được hiển thị như sau -

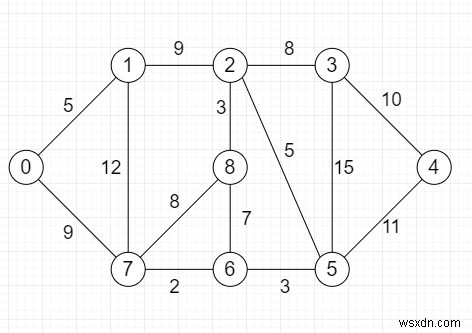
Vì vậy, nếu đầu vào giống như Nguồn =0, k =64, thì đầu ra sẽ là Đúng vì tồn tại một đường dẫn đơn giản 0 đến 7 đến 1 đến 2 đến 8 đến 6 đến 5 đến 3 đến 4, chiều dài đường dẫn này có tổng khoảng cách 68 lớn hơn 64.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định biểu đồ bằng cách sử dụng ma trận kề điều chỉnh của thứ tự các nút x nút và lấp đầy bằng chi phí cạnh

• Định nghĩa một hàm giải quyết (). Điều này sẽ lấy nguồn, k, đường dẫn

• nếu k <=0, thì

  • trả về True

• i:=0

• trong khi tôi không giống với kích thước của adj [source], hãy làm

  • v:=adj [nguồn, i, 0]

  • w:=adj [nguồn, i, 1]

  • i:=i + 1

  • nếu đường dẫn [v] là True thì

    • chuyển sang lần lặp tiếp theo

  • nếu w> =k, thì

    • trả về True

  • path [v]:=True

  • nếu giải quyết (v, k-w, path) là true, thì

    • trả về True

  • path [v]:=False

• trả về Sai

• Từ phương thức chính, thực hiện như sau -

• path:=một danh sách có kích thước giống như các nút, sau đó điền vào các giá trị sai

• đường dẫn [nguồn]:=1

• trả về giải quyết (nguồn, k, đường dẫn)

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

class Graph:
   def __init__(self, nodes):
      self.nodes = nodes
      self.adj = [[] for i in range(nodes)]
   def insert_edge(self,u, v, w):
      self.adj[u].append([v, w])
      self.adj[v].append([u, w])
   def solve(self,source, k, path):
      if (k <= 0):
         return True
      i = 0
      while i != len(self.adj[source]):
         v = self.adj[source][i][0]
         w = self.adj[source][i][1]
         i += 1
         if (path[v] == True):
            continue
         if (w >= k):
            return True
         path[v] = True
         if (self.solve(v, k-w, path)):
            return True
         path[v] = False
      return False
   def is_there_any_path(self,source, k):
      path = [False]*self.nodes
      path[source] = 1
      return self.solve(source, k, path)

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64
print(g.is_there_any_path(source, k))

Đầu vào

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64

Đầu ra

True