Khái niệm
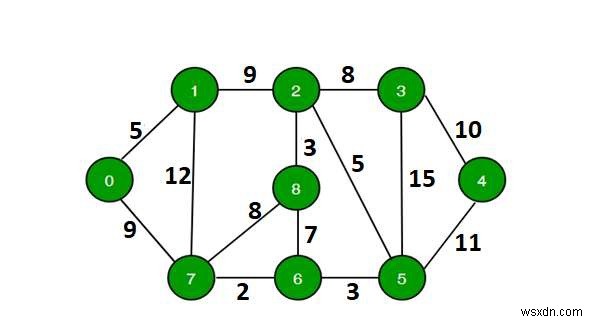
Đối với một đồ thị đã cho, một đỉnh nguồn trong đồ thị và một số k (ở đây k cho biết độ dài đường đi của đồ thị giữa đỉnh nguồn và đỉnh đích), nhiệm vụ của chúng ta là xác định xem có một đường đi đơn giản (không có chu trình nào) bắt đầu hay không. từ nguồn đã cho và kết thúc ở bất kỳ đỉnh nào khác (tức là điểm đến). Biểu đồ được hiển thị như sau -
Đầu vào
Source s = 0, k = 64
Đầu ra
True
Tồn tại một con đường đơn giản 0 -> 7 -> 1-> 2 -> 8 -> 6 -> 5 -> 3 -> 4, có tổng khoảng cách là 68 km lớn hơn 64.
Đầu vào
Source s = 0, k = 70
Đầu ra
False
Trong biểu đồ trên, đường dẫn đơn giản dài nhất có khoảng cách 69 (0 -> 7 -> 1-> 2 -> 3 -> 4 -> 5-> 6 -> 8, đầu ra phải sai đối với bất kỳ đầu vào nào lớn hơn 69.
Phương pháp
Cần lưu ý rằng một điều quan trọng chỉ đơn giản là thực hiện BFS (Tìm kiếm đầu tiên theo chiều rộng) hoặc DFS (Tìm kiếm đầu tiên theo chiều sâu) và chọn cạnh dài nhất ở mỗi bước sẽ không hoạt động. trọng số cao hơn được kết nối thông qua nó.
Bây giờ khái niệm là thực hiện Backtracking. Trong trường hợp này, chúng tôi bắt đầu từ nguồn đã cho; đi qua tất cả các đường từ đỉnh hiện tại. Ở đây, chúng tôi duy trì theo dõi khoảng cách hiện tại từ nguồn. Đã có thể thấy rằng nếu khoảng cách trở nên lớn hơn k, chúng ta trả về true. Nhưng trong trường hợp có các lựa chọn thay thế mà nếu đường dẫn không tạo ra nhiều hơn k khoảng cách, chúng tôi sẽ lùi lại.
Bây giờ câu hỏi được đặt ra là làm thế nào để chúng ta đảm bảo rằng con đường đó đơn giản và chúng ta không quay vòng? Ở đây khái niệm là duy trì theo dõi các đỉnh đường dẫn hiện tại trong một mảng. Trong trường hợp này, bất cứ khi nào chúng tôi thêm một đỉnh vào đường dẫn, chúng tôi xác minh xem nó đã tồn tại hay chưa trong đường dẫn hiện tại. Rõ ràng rằng nếu nó tồn tại, chúng ta sẽ bỏ qua lợi thế.
Ví dụ
// Program to find if there is a simple path with
// weight more than k
#include<bits/stdc++.h>
using namespace std;
// iPair ==> Integer Pair
typedef pair<int, int> iPair;
// Now this class represents a dipathted graph using
// adjacency list representation
class Graph{
int V1; // Indicates no. of vertices
// In this case, in a weighted graph, we need to store vertex
// and weight pair for every edge
list< pair<int, int>> *adj1;
bool pathMoreThanKUtil(int src1, int k, vector<bool>&path1);
public:
Graph(int V1); // Shows constructor
// Shows function to add an edge to graph
void addEdge(int u1, int v1, int w1);
bool pathMoreThanK(int src1, int k);
};
// Used to return true if graph has path more than k length
bool Graph::pathMoreThanK(int src1, int k){
// Used to create a path array with nothing included
// in path
vector<bool> path1(V1, false);
// Used to add source vertex to path
path1[src1] = 1;
return pathMoreThanKUtil(src1, k, path1);
}
// Used to print shortest paths from src to all other vertices
bool Graph::pathMoreThanKUtil(int src1, int k, vector<bool>&path1){
// Now if k is 0 or negative, return true;
if (k <= 0)
return true;
//Used to get all adjacent vertices of source vertex src and
// recursively explore all paths from src.
list<iPair>::iterator i;
for (i = adj1[src1].begin(); i != adj1[src1].end(); ++i){
// Used to get adjacent vertex and weight of edge
int v1 = (*i).first;
int w1 = (*i).second;
// Now if vertex v is already there in path, then
// there is a cycle (we ignore this edge)
if (path1[v1] == true)
continue;
// Now if weight of is more than k, return true
if (w1 >= k)
return true;
// Else add this vertex to path
path1[v1] = true;
// Now if this adjacent can provide a path longer
// than k, return true.
if (pathMoreThanKUtil(v1, k-w1, path1))
return true;
// Backtrack
path1[v1] = false;
}
// Now if no adjacent could produce longer path, return
// false
return false;
}
// Used to allocates memory for adjacency list
Graph::Graph(int V1){
this->V1 = V1;
adj1 = new list<iPair> [V1];
}
//Shows utility function to an edge (u, v) of weight w
void Graph::addEdge(int u1, int v1, int w1){
adj1[u1].push_back(make_pair(v1, w1));
adj1[v1].push_back(make_pair(u1, w1));
}
// Driver program to test methods of graph class
int main(){
// Used to create the graph given in above fugure
int V1 = 9;
Graph g(V1);
// making above shown graph
g.addEdge(0, 1, 5);
g.addEdge(0, 7, 9);
g.addEdge(1, 2, 9);
g.addEdge(1, 7, 12);
g.addEdge(2, 3, 8);
g.addEdge(2, 8, 3);
g.addEdge(2, 5, 10);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 5, 11);
g.addEdge(5, 6, 3);
g.addEdge(6, 7, 2);
g.addEdge(6, 8, 7);
g.addEdge(7, 8, 8);
int src1 = 0;
int k = 70;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
k = 68;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
return 0;
} Đầu ra
No Yes
