Tìm độ dài của đường dẫn liên tiếp dài nhất từ ​​một ký tự bắt đầu nhất định trong C ++

Một ma trận gồm các ký tự khác nhau được đưa ra. Bắt đầu từ một ký tự, chúng ta phải tìm đường đi dài nhất bằng cách duyệt qua tất cả các ký tự lớn hơn ký tự hiện tại. Các ký tự liên tiếp với nhau.

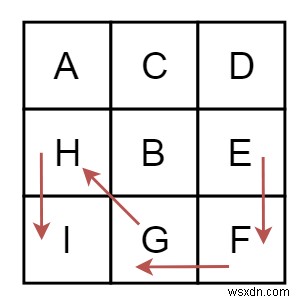
Bắt đầu từ E.

Để tìm đường đi dài nhất, chúng tôi sẽ sử dụng thuật toán Tìm kiếm đầu tiên theo chiều sâu. Trong DFS, một số vấn đề phụ có thể phát sinh nhiều lần. Để tránh phải tính toán nhiều lần các vấn đề phụ đó, chúng tôi sẽ sử dụng phương pháp lập trình động.

Ví dụ

#include<iostream>
#define ROW 3
#define COL 3
using namespace std;
// tool matrices to recur for adjacent cells.
int x[] = {0, 1, 1, -1, 1, 0, -1, -1};
int y[] = {1, 0, 1, 1, -1, -1, 0, -1};
int longestPath[ROW][COL];
char mat[ROW][COL] = {
   {'a','c','d'},
   {'h','b','a'},
   {'i','g','f'}
};
int max(int a, int b){
   return (a>b)?a:b;
}
bool isvalid(int i, int j){
   if (i < 0 || j < 0 || i >= ROW || j >= COL) //when i and j are in range
   return false;
   return true;
}
bool isadjacent(char previous, char current){
   return ((current - previous) == 1); //check current and previous are adjacent or not
}
int findLongestLen(int i, int j, char prev){
   if (!isvalid(i, j) || !isadjacent(prev, mat[i][j]))
      //when already included or not adjacent
      return 0;
   if (longestPath[i][j] != -1)
   return longestPath[i][j]; //subproblems are solved already
   int len = 0; // Initialize result to 0
   for (int k=0; k<8; k++) //find length of the largest path recursively
   len = max(len, 1 + findLongestLen(i + x[k], j + y[k], mat[i][j]));
      return longestPath[i][j] = len; // save the length and return
}
int getLen(char start){
   for(int i = 0; i<ROW; i++)
   for(int j = 0; j<COL; j++)
   longestPath[i][j] = -1; //set all elements to -1
   int len = 0;
   for (int i=0; i<ROW; i++){
      for (int j=0; j<COL; j++){ // check for all possible starting point
         if (mat[i][j] == start) {
            for (int k=0; k<8; k++) //for all eight adjacent cells
               len = max(len, 1 + findLongestLen(i + x[k], j + y[k], start));
            }
         }
   }
   return len;
}
int main() {
   char start;
   cout << "Enter Starting Point (a-i): "; cin >> start;
   cout << "Maximum consecutive path: " << getLen(start);
   return 0;
}

Đầu ra

Enter Starting Point (a-i): e
Maximum consecutive path: 5