Giả sử chúng ta được cho một số thùng và x số quả bóng. Nếu các quả bóng được đưa vào xô, một lực đặc biệt tác động vào bên trong chúng và chúng ta phải tìm ra cách để lực cực đại giữa hai quả bóng là nhỏ nhất. Hợp lực giữa hai quả cầu trong thùng ở vị trí p và q là | p - q |. Đầu vào được cung cấp cho chúng ta là mảng chứa các vị trí xô và số quả bóng x. Chúng ta phải tìm ra lực tối thiểu giữa chúng.
Vì vậy, nếu đầu vào là pos =[2, 4, 6, 8, 10, 12], x =3, thì đầu ra sẽ là 4.
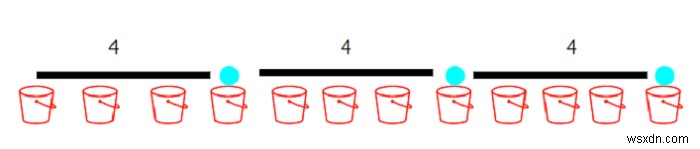
Các quả bóng có thể được đặt vào các vị trí đã cho trong một mảng 12 cái xô. Ba quả bóng có thể được đặt vào các vị trí 4, 8 và 12 và sức mạnh giữa chúng sẽ là 4. Giá trị này không thể tăng thêm nữa.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Định nghĩa một hàm ball_count (). Điều này sẽ mất d
-
và:=1
-
curr:=pos [0]
-
đối với tôi trong phạm vi từ 1 đến n, hãy thực hiện
-
nếu pos [i] - curr> =d, thì
-
ans:=ans + 1
-
curr:=pos [i]
-
-
-
trả lại ans
-
-
n:=kích thước của pos
-
sắp xếp danh sách pos
-
trái:=0
-
right:=pos [-1] - pos [0]
-
trong khi trái
-
mid:=right - giá trị sàn của ((phải - trái) / 2)
-
nếu ball_count (giữa)> =x, thì
-
left:=mid
-
-
nếu không,
-
right:=mid - 1
-
-
-
quay lại bên trái
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def solve(pos, x): n = len(pos) pos.sort() def ball_count(d): ans, curr = 1, pos[0] for i in range(1, n): if pos[i] - curr >= d: ans += 1 curr = pos[i] return ans left, right = 0, pos[-1] - pos[0] while left < right: mid = right - (right - left) // 2 if ball_count(mid) >= x: left = mid else: right = mid - 1 return left print(solve([2, 4, 6, 8, 10, 12], 3))
Đầu vào
[2, 4, 6, 8, 10, 12], 3
Đầu ra
4
