Giả sử chúng ta có một ma trận nhị phân n x n. Chúng ta có thể thực hiện một thao tác trên nó như, ở một bước, chúng ta chọn hai hàng liền kề và hoán đổi chúng. Chúng ta phải đếm số lần hoán đổi tối thiểu được yêu cầu, để tất cả các nút phía trên đường chéo chính của ma trận bằng 0. Nếu không có giải pháp nào như vậy, hãy trả về -1.
Vì vậy, nếu đầu vào giống như
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
thì đầu ra sẽ là 2 vì -
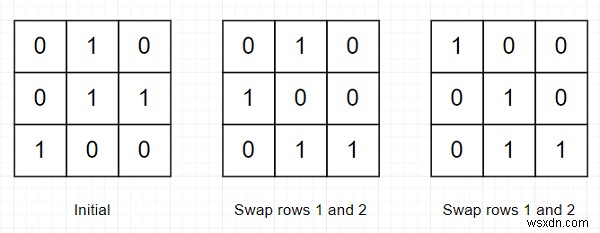
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau:
-
n:=số hàng của ma trận
-
m:=tạo một mảng có kích thước n và điền bằng n
-
đối với tôi trong phạm vi từ 0 đến n - 1, hãy thực hiện
-
đối với j trong phạm vi n-1 đến 0, giảm 1, thực hiện
-
nếu ma trận [i, j] giống 1 thì
-
m [i]:=n-j-1
-
đi ra từ vòng lặp
-
-
-
-
t:=0, ans:=0
-
đối với tôi trong phạm vi từ 0 đến n - 1, hãy thực hiện
-
t:=t + 1
-
cờ:=Sai
-
đối với j trong phạm vi i đến n - 1, thực hiện
-
nếu m [j]> =n-t thì
-
ans:=ans + j-i
-
flag:=True
-
đi ra từ vòng lặp
-
-
-
nếu cờ là sai, thì
-
trả về -1
-
-
cập nhật m [từ chỉ mục i + 1 đến j] theo m [từ chỉ mục i đến j-1]
-
-
trả lại ans
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
def solve(matrix): n = len(matrix) m = [n] * n for i in range(n): for j in range(n-1,-1,-1): if matrix[i][j] == 1: m[i] = n-j-1 break t,ans = 0,0 for i in range(n): t += 1 flag = False for j in range(i,n): if m[j] >= n-t: ans += j-i flag = True break if not flag: return -1 m[i+1:j+1] = m[i:j] return ans matrix = [[0,1,0],[0,1,1],[1,0,0]] print(solve(matrix))
Đầu vào
[[0,1,0],[0,1,1],[1,0,0]]
Đầu ra
2
