Backtracking là một kỹ thuật dựa trên thuật toán để giải quyết vấn đề. Nó sử dụng cách gọi đệ quy để tìm giải pháp bằng cách xây dựng giải pháp từng bước tăng giá trị theo thời gian. Nó loại bỏ các giải pháp không tạo ra giải pháp của vấn đề dựa trên các ràng buộc được đưa ra để giải quyết vấn đề.
Thuật toán bẻ khóa ngược được áp dụng cho một số dạng vấn đề cụ thể,
-
Bài toán quyết định được sử dụng để tìm ra giải pháp khả thi cho vấn đề.
-
Bài toán tối ưu hóa được sử dụng để tìm giải pháp tốt nhất có thể được áp dụng.
-
Bài toán liệt kê được sử dụng để tìm tập hợp tất cả các giải pháp khả thi của bài toán.
Trong vấn đề bẻ khóa ngược, thuật toán cố gắng tìm một đường dẫn trình tự dẫn đến giải pháp có một số điểm kiểm tra nhỏ mà từ đó vấn đề có thể quay ngược trở lại nếu không tìm thấy giải pháp khả thi nào cho vấn đề.
Ví dụ,
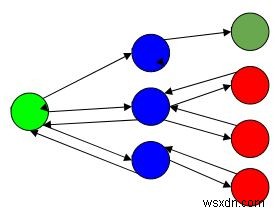
Đây,
Màu xanh lá cây là điểm bắt đầu, màu xanh lam là điểm trung gian, màu đỏ là điểm không có giải pháp khả thi, màu xanh lá cây đậm là giải pháp kết thúc.
Ở đây, khi thuật toán truyền đến điểm kết thúc để kiểm tra xem nó có phải là một giải pháp hay không, nếu nó đúng thì trả về giải pháp, nếu không, nó sẽ lùi lại điểm sau nó một bước để tìm đường đến điểm tiếp theo để tìm giải pháp.
Thuật toán
Bước 1 - nếu current_position là mục tiêu, trả về thành công Bước 2 - else, Bước 3 - nếu current_position là điểm kết thúc, trả về không thành công. Bước 4 - else, nếu current_position không phải là điểm kết thúc, hãy khám phá và lặp lại các bước trên.Hãy sử dụng bài toán bẻ khóa ngược này để tìm giải pháp cho N-Queen Problem .
Trong bài toán N-Queen, chúng ta được đưa ra một bàn cờ NxN và chúng ta phải đặt n quân hậu trên bàn cờ sao cho không có hai quân hậu tấn công nhau. Một quân hậu sẽ tấn công một quân hậu khác nếu nó được đặt ở các điểm ngang, dọc hoặc chéo trên đường của nó. Ở đây, chúng ta sẽ làm bài toán 4 Queen.
Đây, giải pháp là -

Tại đây, đầu ra nhị phân cho bài toán n nữ hoàng với 1 là nữ hoàng cho các vị trí được đặt.
{0, 1, 0, 0} {0, 0, 0, 1} {1, 0, 0, 0} {0, 0, 1, 0}Để giải quyết vấn đề n nữ hoàng, chúng ta sẽ thử đặt quân hậu vào các vị trí khác nhau của một hàng. Và kiểm tra xem nó có đụng độ với các con hoàng hậu khác hay không. Nếu vị trí hiện tại của các nữ hoàng nếu có bất kỳ hai nữ hoàng tấn công nhau. Nếu chúng đang tấn công, chúng tôi sẽ quay lại vị trí trước đó của nữ hoàng và thay đổi vị trí của nó. Và kiểm tra lại cuộc đụng độ của nữ hoàng.
Thuật toán
Bước 1 - Bắt đầu từ vị trí đầu tiên trong mảng.
Bước 2 - Đặt quân hậu vào bảng và kiểm tra. Thực hiện, Bước 2.1 - Sau khi đặt quân hậu, đánh dấu vị trí là một phần của giải pháp và sau đó kiểm tra đệ quy xem điều này có dẫn đến giải pháp hay không. Bước 2.2 - Bây giờ, nếu việc đặt quân hậu không dẫn đến giải pháp và theo dõi, hãy chuyển sang bước (a) và đặt quân hậu sang các hàng khác. Bước 2.3 - Nếu đặt nữ hoàng trả về một dẫn đến giải pháp trả về ĐÚNG. Bước 3 - Nếu tất cả các quân hậu được đặt thì trả về ĐÚNG.Bước 4 - Nếu tất cả các hàng được thử và không tìm thấy giải pháp nào, hãy trả về FALSE.
Bây giờ, hãy sử dụng backtracking để giải quyết Chuột trong mê cung vấn đề -
Trong bài toán chuột trong mê cung, chúng ta với mê cung NxN là vị trí đầu tiên của mê cung, tức là [0] [0] và sẽ kết thúc ở vị trí [n-1] [n-1] của mảng. Trong con đường này, có một số con đường chết không dẫn đến giải pháp.
Sử dụng backtracking trong bài toán này, chúng ta sẽ đi xuống từng bước để đạt được vị trí mục tiêu cuối cùng trong mê cung.
Mảng 2D bên dưới cho biết vấn đề có vẻ như thế nào.

Tại đây các đường đứt nét hiển thị con đường đã đi.
