Vấn đề
Áp dụng phương pháp phát triển phần mềm để giải quyết mọi vấn đề bằng Ngôn ngữ C
Giải pháp
- Tìm nghiệm nguyên của phương trình bậc hai, ax2 + bx + c.
- Sẽ có 2 nghiệm nguyên của phương trình bậc hai đã cho.
Phân tích
Đầu vào - các giá trị a, b, c
Đầu ra - giá trị r1, r2
Quy trình
$ r_ {1} =\ frac {-b + \ sqrt {b ^ 2-4ac}} {2a} $
$ r_ {2} =\ frac {-b- \ sqrt {b ^ 2-4ac}} {2a} $
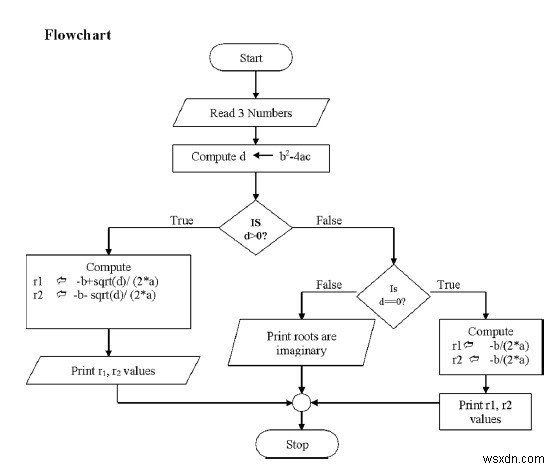
Thiết kế (Thuật toán)
- Bắt đầu
- Đọc các giá trị a, b, c
- Tính d =b2 4ac
- nếu d> 0 thì
- r1 =b + sqrt (d) / (2 * a)
- r2 =b sqrt (d) / (2 * a)
- Ngược lại nếu d =0 thì
- tính toán r1 =-b / 2a, r2 =-b / 2a
- in các giá trị r1, r2
- Ngược lại nếu d <0 thì gốc in là ảo
- Dừng lại
Mã triển khai
# include<stdio.h>
# include<conio.h>
# include<math.h>
main (){
float a,b,c,r1,r2,d;
printf (“enter the values of a b c”);
scanf (“ %f %f %f”, &a, &b, &c);
d= b*b – 4*a*c;
if (d>0){
r1 = -b+sqrt (d) / (2*a);
r2 = -b-sqrt (d) / (2*a);
printf (“The real roots = %f %f”, r1, r2);
}
else if (d= =0){
r1 = -b/(2*a);
r2 = -b/(2*a);
printf (“roots are equal =%f %f”, r1, r2);
}
else
printf(“Roots are imaginary”);
getch ();
} Thử nghiệm
Case 1: enter the values of a b c: 1 4 3 r1 = -1 r2 = -3 Case 2: enter the values of a b c: 1 2 1 r1 = -1 r2 = -1 Case 3: enter the values of a b c: 1 1 4 Roots are imaginary
