Đây là phần 3 trong loạt bài về việc triển khai các thuật toán sắp xếp khác nhau với Ruby. Phần 1 khám phá sắp xếp bong bóng và phần 2 khám phá cách sắp xếp lựa chọn.
Như chúng ta đã thảo luận trong các bài trước của loạt bài này, hiểu cách sắp xếp dữ liệu là một phần không thể thiếu trong bộ công cụ của bất kỳ kỹ sư phần mềm nào. May mắn thay, hầu hết các ngôn ngữ cấp cao hơn, như Ruby, đã có các phương thức tích hợp sẵn có hiệu quả trong việc sắp xếp các mảng. Ví dụ:khi bạn gọi .sort trên một mảng, bạn đang sử dụng quicksort dưới mui xe. Trong bài đăng này, chúng ta sẽ tìm hiểu một thuật toán tương tự để sắp xếp nhanh - sắp xếp hợp nhất. Cả hai thuật toán này đều sử dụng phương pháp "chia để trị". Merge sort được phát minh bởi John von Neumann vào năm 1945. Von Neumann là một nhà khoa học máy tính và nhà vật lý học nổi tiếng, người cũng được biết đến với công việc trong Dự án Manhattan, định lý "mini-max", phương pháp Monte Carlo, v.v.>
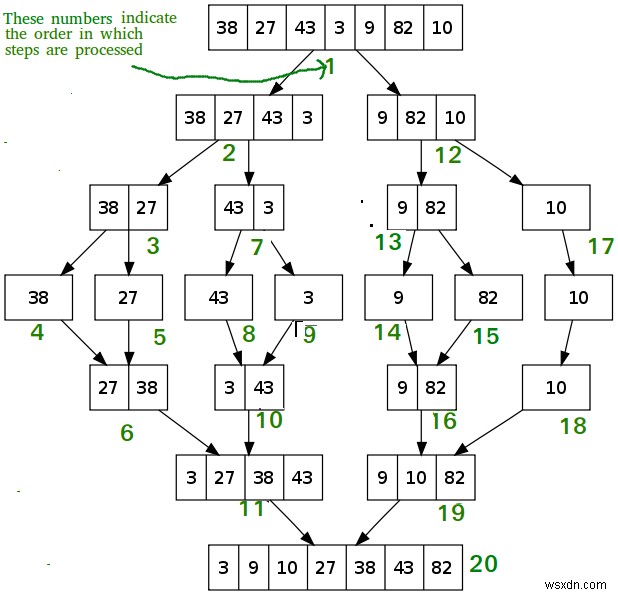
Ở mức cao, thuật toán sắp xếp hợp nhất chia mảng thành hai mảng con lặp đi lặp lại (sử dụng đệ quy) cho đến khi chỉ còn lại một phần tử. Từ đó, các phần tử được "hợp nhất" lại với nhau để tạo thành mảng được sắp xếp cuối cùng. Không giống như sắp xếp bong bóng và các thuật toán tương tự khác, sắp xếp hợp nhất rất khó hiểu nếu không trực quan hóa. Sơ đồ sau đây là minh họa từng bước từ Wikipedia cho thấy cách sắp xếp hợp nhất hoạt động. Tuy nhiên, đừng lo lắng nếu bạn vẫn còn hơi mờ nhạt về những gì đang diễn ra; chúng tôi sẽ làm việc thông qua mã tiếp theo.
Không giống như các thuật toán mà chúng ta đã thảo luận trước đây (tức là bong bóng và lựa chọn), về cơ bản là không thực tế đối với bất kỳ tác vụ thực tế nào, sắp xếp hợp nhất hoạt động tốt hơn nhiều về mặt ký hiệu Big-O. Nếu bạn không quen với ký hiệu Big-O, nó đại diện cho hiệu suất trong trường hợp xấu nhất của các thuật toán khác nhau. Điều này cho phép chúng tôi dễ dàng so sánh các thuật toán dựa trên Big-O của chúng. Ví dụ:một thuật toán có Big-O là O (1) có nghĩa là thời gian chạy trong trường hợp xấu nhất là không đổi khi số phần tử, "n", tăng lên, trong khi một thuật toán có ký hiệu Big-O là O ( n) có nghĩa là thời gian chạy trong trường hợp xấu nhất tăng tuyến tính khi n tăng lên. Điều này có nghĩa là nếu bạn có một mảng với 100 phần tử và phải chọn giữa các thuật toán sắp xếp là O (n) và O (1), bạn sẽ chọn thuật toán O (1) vì O (1) chắc chắn thắng O (100). Cả hai thuật toán sắp xếp bong bóng và lựa chọn đều có trường hợp xấu nhất là O (n ^ 2). Điều này không hữu ích lắm vì nó có nghĩa là thuật toán sẽ hoạt động cực kỳ chậm khi số lượng phần tử tăng lên. Ngược lại, sắp xếp hợp nhất thực hiện ở n log (n), có nghĩa là thuật toán sẽ không hy sinh nhiều hiệu quả như sắp xếp bong bóng hoặc sắp xếp lựa chọn.
Hãy xem qua ví dụ trong sơ đồ. Chúng ta bắt đầu với một mảng [38, 27, 43, 3, 9, 82, 10] và sau đó chia mảng làm đôi cho đến khi chúng ta chỉ còn lại các phần tử duy nhất.
- Chúng tôi chia mảng bắt đầu thành hai nửa:
[38, 27, 43, 3]và[9, 82, 10]. - Chúng tôi lại chia nửa đầu:
[38, 27]và[43, 3]. - Chúng tôi chia nửa đầu thành các phần tử đơn lẻ:
[38],[27],[43]và[3]. - Chúng tôi sắp xếp 38 và 27 để tạo thành
[27, 38]và 48 và 3 để tạo[3, 43]. - Kết hợp những thứ này lại với nhau, chúng ta có
[3, 27, 38, 43]. - Bây giờ, chúng ta chuyển sang nửa sau của mảng ban đầu, là
[9, 82, 10]. Chúng tôi chia nó ra làm đôi và lấy[9, 82]và[10]. - Chúng tôi tách
[9, 82]thành[9]và[82], và sau đó chúng ta có[10], vốn đã là số ít. - Chúng tôi sắp xếp
[9, 82]trở lại với nhau và sau đó hợp nhất[10]quay lại, kết quả là[9, 10, 82]. - Cuối cùng, chúng tôi hợp nhất
[3, 27, 38, 43]và[9, 10, 82]để nhận[3, 9, 10, 27, 38, 43, 82].
Triển khai Ruby
Sau đây là một thuật toán sắp xếp hợp nhất được viết bằng Ruby:
class MergeSort
def sort(numbers)
num_elements = numbers.length
if num_elements <= 1
return numbers
end
half_of_elements = (num_elements / 2).round
left = numbers.take(half_of_elements)
right = numbers.drop(half_of_elements)
sorted_left = sort(left)
sorted_right = sort(right)
merge(sorted_left, sorted_right)
end
def merge(left_array, right_array)
if right_array.empty?
return left_array
end
if left_array.empty?
return right_array
end
smallest_number = if left_array.first <= right_array.first
left_array.shift
else
right_array.shift
end
recursive = merge(left_array, right_array)
[smallest_number].concat(recursive)
end
end
Hãy xem qua những gì đang xảy ra ở đây. Đầu tiên, chúng ta sẽ tập trung vào sort ở trên cùng.
def sort(numbers)
num_elements = numbers.length
if num_elements <= 1
return numbers
end
half_of_elements = (num_elements / 2).round
left = numbers.take(half_of_elements)
right = numbers.drop(half_of_elements)
sorted_left = sort(left)
sorted_right = sort(right)
merge(sorted_left, sorted_right)
end
Mục tiêu của phần mã này là chia đôi các số đã cho cho đến khi chúng ta chỉ còn lại một mục trong mỗi mục. Để xem nó hoạt động, hãy nhận xét dòng cuối cùng (hợp nhất (sorted_left, sorted_right)) và thay vào đó, in ra sorted_left và sorted_right . Chạy chương trình bằng cách chuyển vào mảng ví dụ của chúng tôi, bạn sẽ thấy điều này trong thiết bị đầu cuối của mình:
merge_sort = MergeSort.new
puts merge_sort.sort([38, 27, 43, 3, 9, 82, 10])
ruby ruby-merge-sort.rb
27
43
38
3
9
82
10
Tuyệt quá! Mã của chúng tôi đã lấy mảng ban đầu của chúng tôi và chia nó thành một nửa. Chúng ta hãy xem xét merge phần mã tiếp theo.
def merge(left_array, right_array)
if right_array.empty?
return left_array
end
if left_array.empty?
return right_array
end
smallest_number = if left_array.first <= right_array.first
left_array.shift
else
right_array.shift
end
recursive = merge(left_array, right_array)
[smallest_number].concat(recursive)
end
Đầu tiên, chúng tôi kiểm tra xem một trong hai mảng con có trống hay không. Nếu vậy, chúng ta có thể trả lại cái còn lại. Nếu không, do cả hai mảng con đều không trống, chúng tôi so sánh giá trị của phần tử đầu tiên của mỗi mảng và sau đó dịch chuyển các giá trị được so sánh để ngăn việc tạo ra một vòng lặp vô hạn. Tiếp theo, chúng tôi sử dụng đệ quy (nhiều hơn trong một giây!) Trên mảng ban đầu cho đến khi cuối cùng chúng tôi có thể kết nối hai mảng với nhau, được sắp xếp độc đáo.
Thông tin thêm về đệ quy
Nếu có điều gì đó trông kỳ lạ trong mã của chúng tôi, tôi đoán là dòng này:recursive = merge(left_array, right_array) Chúng tôi đang gọi merge của chúng tôi phương pháp từ bên trong chính nó . Ái chà! Đây là những gì chúng ta gọi là đệ quy - một kỹ thuật trong đó một hàm gọi chính nó một hoặc nhiều lần cho đến khi một điều kiện cụ thể được đáp ứng. Trong trường hợp của chúng tôi, merge sẽ tiếp tục được gọi cho đến khi mảng bên trái hoặc bên phải trống. Nếu bạn muốn tìm hiểu thêm về đệ quy, đây là một ví dụ hướng dẫn cách sử dụng Ruby và đệ quy để viết một hàm cho Chuỗi Fibonacci.
Kết thúc
Tôi hy vọng bạn thích tìm hiểu thêm về sắp xếp hợp nhất! Hiểu cách nó hoạt động ở cấp độ cao, cũng như lý do tại sao nó là một lựa chọn hiệu quả hơn bong bóng hoặc phân loại lựa chọn có thể sẽ hữu ích trong các cuộc phỏng vấn xin việc hoặc các nhiệm vụ hàng ngày của bạn. Ngoài ra, có một số biến thể sắp xếp hợp nhất mà bạn có thể đọc thêm về nó trên Wikipedia nếu bạn quan tâm. Cho đến lần sau ... chúc bạn sắp xếp vui vẻ!
