Lưu ý:Đây là phần 2 của loạt bài xem xét các thuật toán sắp xếp khác nhau với Ruby. Phần 1 đã khám phá sắp xếp bong bóng.
Trong bài đăng này, tôi sẽ hướng dẫn cách triển khai thuật toán sắp xếp lựa chọn với Ruby. Sắp xếp lựa chọn là một thuật toán sắp xếp so sánh tại chỗ. Điều này có nghĩa là các mục được sắp xếp có cùng dung lượng với các mục gốc. Trước khi chúng ta đi xa hơn, điều quan trọng cần lưu ý là thuật toán sắp xếp lựa chọn không được sử dụng phổ biến trong thực tế trừ khi tập dữ liệu nhỏ (tức là 10-20 phần tử). Tuy nhiên, đó là một thuật toán khởi đầu tuyệt vời để học và hiểu, tương tự như học cách đi xe ba bánh trước xe đạp, nếu bạn muốn. Việc triển khai có thể hiển thị trên một thử thách mã hóa cho một cuộc phỏng vấn việc làm hoặc bạn có thể được yêu cầu giải thích tại sao một thuật toán như sắp xếp lựa chọn sẽ không thực tế lắm trên một tập dữ liệu lớn. Sắp xếp lựa chọn thường hoạt động tốt hơn sắp xếp bong bóng, đây là thuật toán đầu tiên chúng tôi xem xét trong loạt bài này.
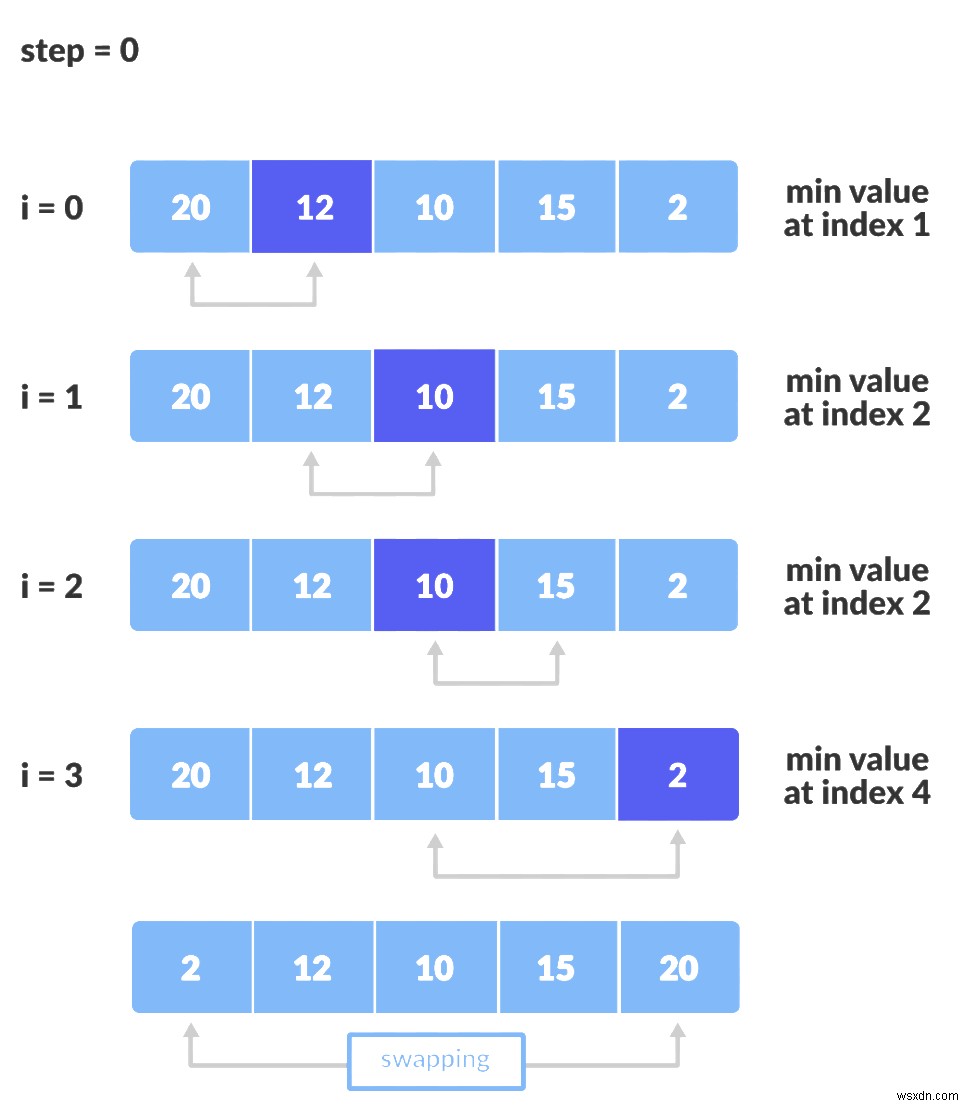
Ở cấp độ cao, sắp xếp lựa chọn chia mảng thành hai phần:một nửa được sắp xếp và phần còn lại thì không. Khi bắt đầu, phần được sắp xếp trống và phần chưa được sắp xếp chứa tất cả các phần tử. Sắp xếp lựa chọn sử dụng hai vòng lặp; vòng lặp ngoài lặp n lần, với n là số phần tử trong mảng. Chúng tôi ngay lập tức đặt "chỉ số tối thiểu" cho phần tử đầu tiên và sau đó sử dụng vòng lặp khác để so sánh các phần tử, hoán đổi chỉ số tối thiểu nếu phần tử liền kề nhỏ hơn mức tối thiểu hiện tại.
Nếu điều này khó làm theo, đừng lo lắng! Tiếp theo, chúng ta sẽ xem xét một ví dụ thực tế. :)
Từng bước
Hãy bắt đầu với một mảng có các phần tử sau:[10, 30, 27, 7, 33, 15, 40, 50]
Lặp lại một lần:Tìm số nhỏ nhất
Trong trường hợp này, số nhỏ nhất là 7 , vì vậy chúng tôi đặt nó ở đầu và di chuyển 10 đến nơi 7 là. Mảng của chúng ta bây giờ trông giống như sau:[7, 30, 27, 10, 33, 15, 40, 50]
Lặp lại hai:Tìm số nhỏ nhất tiếp theo
Bắt đầu từ phần tử ở vị trí chỉ mục 1 (hãy nhớ rằng các mảng được lập chỉ mục 0), hãy tìm phần tử nhỏ nhất tiếp theo
Trong trường hợp này, nó là 10. Di chuyển 10 đến vị trí thứ hai trong mảng và di chuyển 30 đến nơi 10 là. Mảng kết quả là:[7, 10, 27, 30, 33, 15, 40, 50]
Từ đây, chúng tôi tiếp tục quá trình chính xác này cho đến khi mảng của chúng tôi được sắp xếp đầy đủ. Dưới đây, bạn có thể thấy các mảng kết quả sau các lần lặp tiếp theo.
Lặp lại ba:
[7, 10, 15, 30, 33, 27, 40, 50]
Lặp lại bốn:
[7, 10, 15, 27, 33, 30, 40, 50]
Lặp lại năm:
[7, 10, 15, 27, 30, 33, 40, 50]
Chơi lô tô! Chúng tôi được sắp xếp!
Nếu bạn là người học trực quan hơn, đây là ví dụ về cách sắp xếp lựa chọn sẽ hoạt động với một mảng []
 Tín dụng ảnh
Tín dụng ảnh
Triển khai Ruby
Đây là một hàm sắp xếp lựa chọn được viết bằng Ruby:
def selection_sort(array)
n = array.length - 1
n.times do |i|
min_index = i
for j in (i + 1)..n
min_index = j if array[j] < array[min_index]
end
array[i], array[min_index] = array[min_index], array[i] if min_index != i
end
puts array
end
Hãy xem cách này hoạt động như thế nào.
Đầu tiên, chúng tôi đặt n bằng số phần tử. Hãy nhớ rằng, chúng ta cần phải trừ đi một vì các mảng được lập chỉ mục 0.
Tiếp theo, chúng tôi tạo vòng lặp bên ngoài, vòng lặp này sẽ chạy n lần.
min_index = i
Ở đây, chúng tôi đang đặt chỉ số tối thiểu cho phần tử ở vị trí đầu tiên.
for j in (i + 1)..n
Tiếp theo, chúng tôi tạo vòng lặp bên trong của chúng tôi. Dòng này có nội dung "đối với phần tử ở vị trí thứ hai đến phần tử thứ n, hãy làm những gì sau". Nếu bạn không quen thuộc với .. toán tử, nó tạo ra một phạm vi từ điểm bắt đầu đến điểm cuối, bao gồm. Ví dụ:1..10 tạo phạm vi từ 1 đến 10, bao gồm cả.
min_index = j if array[j] < array[min_index]
Bên trong vòng lặp này, chúng tôi đặt min_index thành một phần tử mới nếu nó nhỏ hơn min_index hiện tại .
array[i], array[min_index] = array[min_index], array[i] if min_index != i
Bên ngoài vòng lặp bên trong của chúng tôi, chúng tôi xem xét liệu min_index hiện tại bằng i . Nếu điều này là đúng, chúng ta cần xáo trộn các yếu tố của mình. Chúng tôi đặt array[i] thành array[min_index] và array[min_index] thành array[i] . Ở đây, chúng tôi đang thực hiện "hoán đổi" giống như chúng tôi đã làm trong ví dụ của chúng tôi.
Cuối cùng, khi chúng tôi hoàn thành, chúng tôi xuất ra mảng của mình, hiện đã được sắp xếp!
Tập hợp tất cả cùng nhau
Đây là chương trình đầy đủ của tôi:
def selection_sort(array)
n = array.length - 1
n.times do |i|
min_index = i
for j in (i + 1)..n
min_index = j if array[j] < array[min_index]
end
array[i], array[min_index] = array[min_index], array[i] if min_index != i
end
puts array
end
array = [10, 30, 27, 7, 33, 15, 40, 50]
selection_sort(array)
Đang chạy ruby ruby-selection-sort.rb từ thiết bị đầu cuối cho kết quả như sau:
7
10
15
27
30
33
40
50
Tuyệt vời!
Hiểu tại sao Sắp xếp Lựa chọn không hiệu quả
Một cách để đo lường hiệu quả của thuật toán là xem xét "ký hiệu Big-O"; điều này thể hiện hiệu suất trong trường hợp xấu nhất để các thuật toán có thể được so sánh. Ví dụ:một thuật toán có Big-O là O (1) có nghĩa là thời gian chạy trong trường hợp xấu nhất là không đổi khi số phần tử, "n", tăng lên, trong khi một thuật toán có ký hiệu Big-O là O (n ) có nghĩa là thời gian chạy trong trường hợp xấu nhất tăng tuyến tính khi n tăng lên. Điều này có nghĩa là nếu bạn có một mảng với 100 phần tử và phải chọn giữa các thuật toán sắp xếp là O (n) và O (1), bạn sẽ chọn thuật toán O (1) vì O (1) chắc chắn thắng O (100).
Giống như sắp xếp bong bóng, sắp xếp lựa chọn có độ phức tạp trung bình và trường hợp xấu nhất là O (n ^ 2) do các vòng lặp lồng nhau. Điều này có nghĩa là hiệu quả của nó giảm đáng kể khi số lượng phần tử tăng lên.
Kết thúc
Tất cả những điều được xem xét, sắp xếp lựa chọn vẫn là một thuật toán thú vị có thể bật lên trong một thử thách mã hóa. Hoặc, bạn có thể được cung cấp một chức năng sắp xếp lựa chọn và được hỏi ký hiệu Big-O là gì và tại sao. Hy vọng rằng, các ví dụ trong bài viết này sẽ giúp bạn sẵn sàng giải quyết một trong hai trường hợp.
