Trong cây ảo, một số cạnh được coi là rắn và một số được coi là gạch ngang. Việc rải thông thường chỉ được thực hiện trong các cây rắn. Để hiển thị tại một nút y trong cây ảo, phương pháp sau được thực hiện.
Thuật toán xem xét cây ba lần, một lần trong mỗi lần vượt qua và thay đổi nó. Trong lần vượt qua đầu tiên, bằng cách chỉ xuất hiện trong các liên kết, bắt đầu từ nút y, đường dẫn từ y đến gốc của cây tổng thể, trở nên đứt nét. Đường dẫn này được tạo ra vững chắc bằng cách nối. Một splay cuối cùng tại nút y bây giờ sẽ tạo y là gốc của cây. Ít chính thức hơn, thuật toán được giải thích như sau
Thuật toán cho Splay (y)
Vượt qua 1 Đi bộ lên cây ảo, nhưng quá trình ghép chỉ được thực hiện trong cây con vững chắc. Khi kết thúc quá trình vượt qua này, đường dẫn từ y đến gốc sẽ trở thành dấu gạch ngang.
Vượt qua 2 Đi lên từ nút y, nối từng tổ tiên thích hợp của y. Khi kết thúc bước này, đường dẫn từ y đến gốc trở nên vững chắc. Ngoại trừ điều đó, nút y và tất cả các nút con của nó trong cây ban đầu (nút trước khi vượt qua 1) giờ trở thành nút con bên trái.
Vượt qua 3 Đi lên từ nút y đến gốc, hiển thị theo kiểu bình thường.
Điều này cho phép chúng tôi sử dụng kiến thức trước đây để cải thiện ước tính xác suất của chúng tôi. Đối với bộ lá đã cho. Vì vậy, mục tiêu là tạo một cây với trọng lượng đường dẫn bên ngoài tối thiểu.
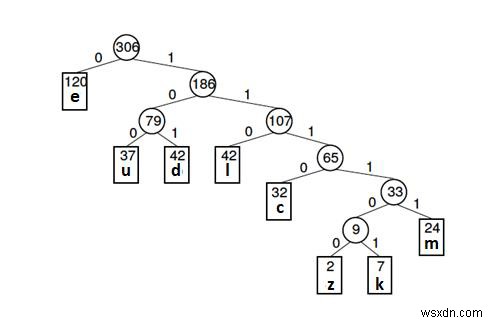
Ví dụ được đưa ra dưới đây
Bảng tần suất thư
| Thư | z | k | m | c | u | d | l | đ |
| Tần suất | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
Mã Huffman
| Thư | Tần suất | Mã | Bits |
|---|---|---|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 37100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
Cây Huffman (ví dụ trên) được đưa ra dưới đây