Kí hiệu tiệm cận
Các ký hiệu tiệm cận được sử dụng để biểu thị sự phức tạp của các thuật toán để phân tích tiệm cận. Các ký hiệu này là công cụ toán học để biểu diễn sự phức tạp. Có ba ký hiệu thường được sử dụng.
Ký hiệu Big Oh
Ký hiệu Big-Oh (O) đưa ra giới hạn trên cho một hàm f (n) trong một hệ số không đổi.

Ta viết f (n) =O (g (n)), Nếu có các hằng số dương n0 và c sao cho, ở bên phải n0 thì f (n) luôn nằm trên hoặc dưới c * g (n).
O (g (n)) ={f (n):Tồn tại hằng số dương c và n0 sao cho 0 ≤ f (n) ≤ c g (n), với mọi n ≥ n0}
Ký hiệu Omega lớn
Ký hiệu Big-Omega (Ω) cung cấp giới hạn dưới cho một hàm f (n) trong một hệ số không đổi.
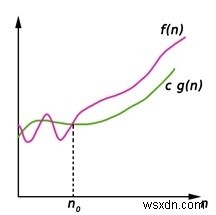
Ta viết f (n) =Ω (g (n)), Nếu có các hằng số dương n0 và c sao cho, ở bên phải n0 thì f (n) luôn nằm trên hoặc trên c * g (n).
Ω (g (n)) ={f (n):Tồn tại hằng số dương c và n0 sao cho 0 ≤ c g (n) ≤ f (n), với mọi n ≥ n0}
Ký hiệu Theta lớn
Ký hiệu Big-Theta (Θ) cung cấp giới hạn cho một hàm f (n) trong một hệ số không đổi.
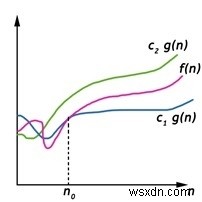
Ta viết f (n) =Θ (g (n)), Nếu tồn tại các hằng số dương n0 và c1 và c2 sao cho, ở bên phải n0 f (n) luôn nằm giữa c1 * g (n) và c2 * g (n) bao gồm.
Θ (g (n)) ={f (n):Tồn tại hằng số dương c1, c2 và n0 sao cho 0 ≤ c1 g (n) ≤ f (n) ≤ c2 g (n), với mọi n ≥ n0}
