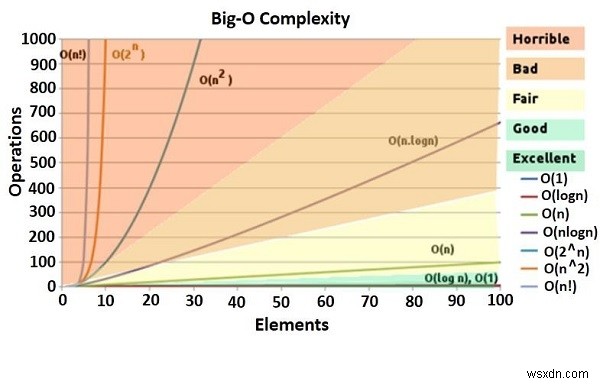
Phân tích tiệm cận
Sử dụng phân tích tiệm cận, chúng ta có thể có được ý tưởng về hiệu suất của thuật toán dựa trên kích thước đầu vào. Chúng ta không nên tính toán thời gian chạy chính xác, nhưng chúng ta nên tìm mối quan hệ giữa thời gian chạy và kích thước đầu vào. Chúng ta nên theo dõi thời gian chạy khi kích thước đầu vào được tăng lên.
Đối với độ phức tạp của không gian, mục tiêu của chúng tôi là có được mối quan hệ hoặc hàm mà có bao nhiêu không gian trong bộ nhớ chính được sử dụng để hoàn thành thuật toán.
Hành vi tiệm cận
Đối với một hàm f (n) hành vi tiệm cận là sự tăng trưởng của f (n) khi n lớn lên. Giá trị đầu vào nhỏ không được xem xét. Nhiệm vụ của chúng tôi là tìm ra bao nhiêu thời gian để có giá trị lớn của đầu vào.
Ví dụ, f (n) =c * n + k là độ phức tạp thời gian tuyến tính. f (n) =c * n 2 + k là độ phức tạp thời gian bậc hai.
Việc phân tích các thuật toán có thể được chia thành ba trường hợp khác nhau. Các trường hợp như sau -
Trường hợp tốt nhất - Ở đây giới hạn dưới của thời gian chạy được tính toán. Nó mô tả hoạt động của thuật toán trong các điều kiện tối ưu.
Trường hợp trung bình - Trong trường hợp này ta tính vùng giữa cận trên và cận dưới của thời gian chạy thuật toán. Trong trường hợp này, số lượng hoạt động được thực thi không phải là tối thiểu và không phải là tối đa.
Trường hợp tồi tệ nhất - Trong trường hợp này ta tính cận trên của thời gian chạy các thuật toán. Trong trường hợp này, số lượng tối đa các hoạt động được thực thi.