Độ phức tạp của thời gian là một trong những khái niệm thú vị nhất mà bạn có thể học được từ khoa học máy tính và bạn không cần bằng cấp để hiểu nó!
Thật thú vị vì nó giúp bạn biết tại sao một thuật toán hoặc chương trình cụ thể có thể chậm &bạn có thể làm gì để làm cho nó nhanh hơn.
Bạn có thể áp dụng điều này cho mã của riêng mình.
Điều này vượt xa tất cả các thuật toán ưa thích mà bạn tìm thấy trong sách khoa học máy tính, như tôi sẽ chứng minh cho bạn ở phần sau của bài viết này.
Nhưng trước tiên chúng ta cần nói về điều gì là chậm và điều gì là nhanh.
Chậm so với Nhanh
Việc sắp xếp 1 triệu số trong 150 mili giây (mili giây) là chậm hay nhanh?
Tôi nghĩ rằng điều đó khá nhanh, nhưng đây không phải là câu hỏi mà sự phức tạp về thời gian đang cố gắng trả lời.
Chúng tôi muốn biết thuật toán sẽ hoạt động như thế nào khi “kích thước đầu vào” tăng lên.
Khi chúng ta nói về "kích thước đầu vào", chúng ta đang nói về các đối số cho hàm hoặc phương thức. Nếu một phương thức nhận một chuỗi làm đối số thì đó là đầu vào và độ dài của chuỗi là kích thước đầu vào.
Ký hiệu Big O
Với ký hiệu Big O, chúng ta có thể phân loại các thuật toán theo hiệu suất của chúng.
Nó trông như thế này:
O(1)
Trong trường hợp này O(1) đại diện cho một thuật toán "thời gian không đổi".
Điều đó có nghĩa là thuật toán sẽ luôn mất cùng một khoảng thời gian để hoàn thành công việc của nó, bất kể nó phải làm bao nhiêu công việc.
Một cái khác là "thời gian tuyến tính":
O(n)
Trong đó “n” đại diện cho kích thước của đầu vào (kích thước chuỗi, kích thước mảng, v.v.). Điều này có nghĩa là thuật toán sẽ hoàn thành công việc của nó theo quan hệ 1:1 với kích thước đầu vào, vì vậy việc tăng gấp đôi kích thước đầu vào cũng sẽ tăng gấp đôi thời gian cần để hoàn thành công việc.
Đây là bảng :
| Ký hiệu | Tên | Mô tả |
|---|---|---|
| O (1) | Không đổi | Luôn mất thời gian như nhau. |
| O (log n) | Logarit | Khối lượng công việc được chia cho 2 sau mỗi lần lặp lại vòng lặp (tìm kiếm nhị phân). |
| O (n) | Tuyến tính | Thời gian hoàn thành công việc tăng theo mối quan hệ 1-1 với kích thước đầu vào. |
| O (n log n) | Dạng tuyến tính | Đây là vòng lặp lồng nhau, trong đó vòng lặp bên trong chạy trong log n thời gian. Ví dụ bao gồm quicksort, mergesort &heapsort. |
| O (n ^ 2) | bậc hai | Thời gian hoàn thành công việc tăng theo input size ^ 2 quan hệ. Bạn có thể nhận ra điều này bất cứ khi nào bạn có một vòng lặp đi qua tất cả các phần tử &mọi lần lặp của vòng lặp cũng đi qua mọi phần tử. Bạn có một vòng lặp lồng nhau. |
| O (n ^ 3) | Khối | Giống với n^2 , nhưng thời gian phát triển theo n^3 quan hệ với kích thước đầu vào. Tìm một vòng lặp lồng nhau ba lần để nhận ra vòng lặp này. |
| O (2 ^ n) | Hàm mũ | Thời gian hoàn thành công việc tăng theo 2 ^ input size quan hệ. Điều này chậm hơn nhiều so với n^2 , vì vậy đừng nhầm lẫn chúng! Một ví dụ là thuật toán fibonacci đệ quy. |
Phân tích thuật toán
Bạn có thể bắt đầu phát triển trực giác của mình cho điều này nếu bạn nghĩ về đầu vào là một mảng các phần tử “n”.
Hãy tưởng tượng rằng bạn muốn tìm tất cả các phần tử là số chẵn, cách duy nhất để làm điều này là đọc từng phần tử một lần để xem nó có phù hợp với điều kiện hay không.
[1,2,3,4,5,6,7,8,9,10].select(&:even?)
Bạn không thể bỏ qua các số vì bạn có thể bỏ lỡ một số số mà bạn đang tìm kiếm, do đó, điều này làm cho thuật toán này trở thành một thuật toán thời gian tuyến tính O(n) .
3 giải pháp khác nhau cho cùng một vấn đề
Phân tích các ví dụ riêng lẻ rất thú vị, nhưng điều thực sự giúp hiểu được ý tưởng này là cách chúng ta có thể giải quyết cùng một vấn đề bằng cách sử dụng các giải pháp khác nhau.
Chúng ta sẽ khám phá 3 ví dụ mã cho trình kiểm tra giải pháp Scrabble.
Scrabble là một trò chơi cung cấp một danh sách các nhân vật (như ollhe ) yêu cầu bạn tạo các từ (như hello ) bằng cách sử dụng các ký tự này.
Đây là giải pháp đầu tiên :
def scramble(characters, word)
word.each_char.all? { |c| characters.count(c) >= word.count(c) }
end
Bạn có biết độ phức tạp về thời gian của mã này là gì không? Chìa khóa nằm trong count , vì vậy hãy đảm bảo rằng bạn hiểu phương pháp đó làm gì.
Câu trả lời là:O(n^2) .
Và lý do cho điều đó là với each_char chúng ta sẽ xem xét tất cả các ký tự trong chuỗi word . Chỉ riêng điều đó sẽ là một thuật toán thời gian tuyến tính O(n) , nhưng bên trong khối chúng ta có count phương pháp.
Phương thức này thực sự là một vòng lặp khác lặp lại tất cả các ký tự trong chuỗi để đếm chúng.
Giải pháp thứ hai
Được rồi.
Làm thế nào chúng ta có thể làm tốt hơn? Có cách nào để tiết kiệm cho chúng tôi một số vòng lặp không?
Thay vì đếm các ký tự mà chúng tôi có thể xóa chúng, theo cách đó, chúng tôi sẽ có ít ký tự hơn.
Đây là giải pháp thứ hai :
def scramble(characters, word)
characters = characters.dup
word.each_char.all? { |c| characters.sub!(c, "") }
end
Cái này thú vị hơn một chút. Điều này sẽ nhanh hơn nhiều so với count phiên bản trong trường hợp tốt nhất, trong đó các ký tự chúng tôi đang tìm kiếm nằm gần đầu chuỗi.
Nhưng khi tất cả các ký tự đều ở cuối, theo thứ tự ngược lại với cách chúng được tìm thấy trong word , hiệu suất sẽ tương tự như hiệu suất của count phiên bản, vì vậy chúng ta có thể nói rằng đây vẫn là một O(n^2) thuật toán.
Chúng tôi không phải lo lắng về trường hợp không có ký tự nào trong word đều khả dụng, bởi vì all? phương thức sẽ dừng ngay sau khi sub! trả về false . Nhưng bạn sẽ chỉ biết điều này nếu bạn đã nghiên cứu sâu về Ruby, vượt xa những gì mà các khóa học Ruby thông thường cung cấp cho bạn.
Hãy thử với một cách tiếp cận khác
Điều gì sẽ xảy ra nếu chúng ta loại bỏ bất kỳ loại vòng lặp nào bên trong khối? Chúng ta có thể làm điều đó với một hàm băm.
def scramble(characters, word)
available = Hash.new(1)
characters.each_char { |c| available[c] += 1 }
word.each_char.all? { |c| available[c] -= 1; available[c] > 0 }
end
Đọc &ghi giá trị băm là O(1) hoạt động, có nghĩa là nó khá nhanh, đặc biệt là so với lặp lại.
Chúng tôi vẫn có hai vòng lặp :
Một để xây dựng bảng băm và một để kiểm tra nó. Vì các vòng lặp này không được lồng vào nhau nên đây là một O(n) thuật toán.
Nếu chúng tôi đánh giá 3 giải pháp này, chúng tôi có thể thấy rằng phân tích của chúng tôi phù hợp với kết quả:
Số lượnghash 1.216667 0.000000 1.216667 ( 1.216007) sub 6.240000 1.023333 7.263333 ( 7.268173) count 222.866644 0.073333 222.939977 (223.440862)
Đây là biểu đồ đường:
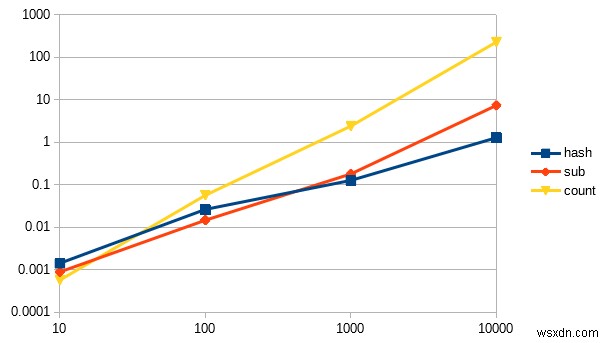
Lưu ý một số điều :
- Trục Y (dọc) biểu thị thời gian mất bao nhiêu giây để hoàn thành công việc, trong khi trục X (ngang) biểu thị kích thước đầu vào.
- Đây là biểu đồ logarit, nén các giá trị trong một phạm vi nhất định, nhưng trên thực tế là
countđường dốc hơn rất nhiều. - Lý do tôi đặt biểu đồ này thành biểu đồ logarit là để bạn có thể đánh giá cao hiệu ứng thú vị, với kích thước đầu vào rất nhỏ
countthực sự nhanh hơn!
Tóm tắt
Bạn đã học về độ phức tạp thời gian của thuật toán, ký hiệu O lớn và phân tích độ phức tạp thời gian. Bạn cũng đã thấy một vài ví dụ trong đó chúng tôi so sánh các giải pháp khác nhau cho cùng một vấn đề và phân tích hiệu suất của chúng.
Hy vọng bạn đã học được điều gì đó mới và thú vị!
Nếu bạn đã chia sẻ bài đăng này trên phương tiện truyền thông xã hội và đăng ký nhận bản tin nếu bạn chưa đăng ký để tôi có thể gửi cho bạn nhiều nội dung như thế này hơn.
Cảm ơn vì đã đọc.
