Thuật toán Floyd Warshall

Thuật toán Floyd-Warshall được sử dụng để tìm tất cả các cặp bài toán đường đi ngắn nhất từ ​​một đồ thị có trọng số cho trước. Kết quả của thuật toán này, nó sẽ tạo ra một ma trận, sẽ đại diện cho khoảng cách tối thiểu từ bất kỳ nút nào đến tất cả các nút khác trong biểu đồ.

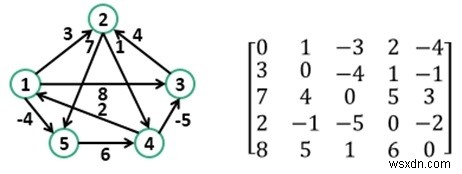
Lúc đầu, ma trận sản lượng giống như ma trận chi phí đã cho của đồ thị. Sau đó, ma trận đầu ra sẽ được cập nhật với tất cả các đỉnh k là đỉnh trung gian.

Độ phức tạp về thời gian của thuật toán này là O (V ^ 3), trong đó V là số đỉnh trong đồ thị.

Đầu vào và Đầu ra

Input: The cost matrix of the graph.
0 3 6 ∞ ∞ ∞ ∞
3 0 2 1 ∞ ∞ ∞
6 2 0 1 4 2 ∞
∞ 1 1 0 2 ∞ 4
∞ ∞ 4 2 0 2 1
∞ ∞ 2 ∞ 2 0 1
∞ ∞ ∞ 4 1 1 0

Output:
Matrix of all pair shortest path.
0 3 4 5 6 7 7
3 0 2 1 3 4 4
4 2 0 1 3 2 3
5 1 1 0 2 3 3
6 3 3 2 0 2 1
7 4 2 3 2 0 1
7 4 3 3 1 1 0

Thuật toán

floydWarshal(cost)

Đầu vào - Ma trận chi phí của Đồ thị đã cho.

Đầu ra: Ma trận để tìm đường đi ngắn nhất giữa bất kỳ đỉnh nào đến đỉnh bất kỳ.

Begin
   for k := 0 to n, do
      for i := 0 to n, do
         for j := 0 to n, do
            if cost[i,k] + cost[k,j] < cost[i,j], then
               cost[i,j] := cost[i,k] + cost[k,j]
         done
      done
   done
   display the current cost matrix
End

Ví dụ

#include<iostream>
#include<iomanip>
#define NODE 7
#define INF 999
using namespace std;

//Cost matrix of the graph
int costMat[NODE][NODE] = {
   {0, 3, 6, INF, INF, INF, INF},
   {3, 0, 2, 1, INF, INF, INF},
   {6, 2, 0, 1, 4, 2, INF},
   {INF, 1, 1, 0, 2, INF, 4},
   {INF, INF, 4, 2, 0, 2, 1},
   {INF, INF, 2, INF, 2, 0, 1},
   {INF, INF, INF, 4, 1, 1, 0}
};

void floydWarshal() {
   int cost[NODE][NODE];    //defind to store shortest distance from any node to any node
   for(int i = 0; i<NODE; i++)
      for(int j = 0; j<NODE; j++)
         cost[i][j] = costMat[i][j];     //copy costMatrix to new matrix

   for(int k = 0; k<NODE; k++) {
      for(int i = 0; i<NODE; i++)
         for(int j = 0; j<NODE; j++)
            if(cost[i][k]+cost[k][j] < cost[i][j])
               cost[i][j] = cost[i][k]+cost[k][j];
   }

   cout << "The matrix:" << endl;
   for(int i = 0; i<NODE; i++) {
      for(int j = 0; j<NODE; j++)
         cout << setw(3) << cost[i][j];
      cout << endl;
   }
}

int main() {
   floydWarshal();
}

Đầu ra

The matrix:
0  3  5  4  6  7  7
3  0  2  1  3  4  4
5  2  0  1  3  2  3
4  1  1  0  2  3  3
6  3  3  2  0  2  1
7  4  2  3  2  0  1
7  4  3  3  1  1  0