Số điểm ban đầu tối thiểu để đến đích

Để bắt đầu từ góc trên cùng bên trái của một lưới nhất định, người ta phải đạt đến góc dưới cùng bên phải. Mỗi ô trong lưới chứa một số, số có thể dương hoặc âm. Khi một người đến ô (i, j), số lượng mã thông báo mà anh ta có, có thể tăng hoặc giảm cùng với các giá trị của ô đó. Chúng tôi phải tìm số lượng mã thông báo ban đầu tối thiểu được yêu cầu để hoàn thành hành trình.

Có một số quy tắc -

• Chúng ta có thể di chuyển sang phải hoặc xuống dưới cùng.
• Chúng tôi không thể di chuyển đến ô (i, j) nếu tổng số mã thông báo của chúng tôi nhỏ hơn giá trị của (i, j).
• Chúng ta phải đến đích với những điểm tích cực tối thiểu.

Đầu vào và Đầu ra

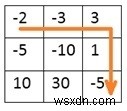
Input:
The token for each room as a matrix.
-2  -3  3
-5 -10  1
10  30 -5

Output:
The minimum token required to start the journey. For this example, the required token is 7.

Thuật toán

minInitTokens(matrix)

Đầu vào: Ma trận mã thông báo cho mỗi phòng.

Đầu ra - cần có mã thông báo tối thiểu để đạt được điểm xuất phát đến đích.

Begin
   define matrix minToken of size same as matrix
   m := number of rows in matrix
   n := number of columns in matrix

   if matrix[m-1, n-1] > 0, then
      minToken[m-1, n-1] := 0
   else
      minToken[m-1, n-1] := 1 + absolute value of matrix[m-1, n-1]

   for i := m-2 down to 0, do
      minToken[i, n-1] := maximum of 1 and (minToken[i+1, n-1]-matrix[i,n-1])
   done

   for j := n-2 down to 0, do
      minToken[m-1, j] := maximum of 1 and (minToken[m-1, j+1]-matrix[m-1, j])
   done

   for i := m-2 down to 0, do
      for j := n-2 down to 0, do
         rem := minimum of minToken[i+1, j] and minToken[i, j+1]
         minPoint[i, j] := maximum of 1 and (rem – matrix[i,j])
      done
   done

   return minToken[0, 0]
End

Ví dụ

#include<iostream>
#include<cmath>
#define ROW 3
#define COL 3
using namespace std;

int tokens[ROW][COL] = {
   {-2,-3,3},
   {-5,-10,1},
   {10,30,-5}
};

int max(int a, int b) {
   return (a>b)?a:b;
}

int minInitPoints() {
   int minToken[ROW][COL];
   int m = ROW, n = COL;
   
   minToken[m-1][n-1] = tokens[m-1][n-1] > 0? 1: abs(tokens[m-1][n-1]) + 1;
   
   for (int i = m-2; i >= 0; i--)    //from last row to first row, fill points
      minToken[i][n-1] = max(minToken[i+1][n-1] - tokens[i][n-1], 1);
   
   for (int j = n-2; j >= 0; j--)    //fill last column to first column, fill points
      minToken[m-1][j] = max(minToken[m-1][j+1] - tokens[m-1][j], 1);

   for (int i=m-2; i>=0; i--) {
      for (int j=n-2; j>=0; j--) {
         int remPoint = min(minToken[i+1][j], minToken[i][j+1]);    //calculate remaining points
         minToken[i][j] = max(remPoint - tokens[i][j], 1);
      }
   }
   return minToken[0][0];
}

int main() {
   cout << "Minimum Points Required: " << minInitPoints();
}

Đầu ra

Minimum Points Required: 7