Điểm tối đa trên một dòng trong C ++

Giả sử chúng ta có một mặt phẳng 2D. Chúng ta phải tìm số điểm lớn nhất nằm trên cùng một đường thẳng. Vì vậy, nếu các điểm như -

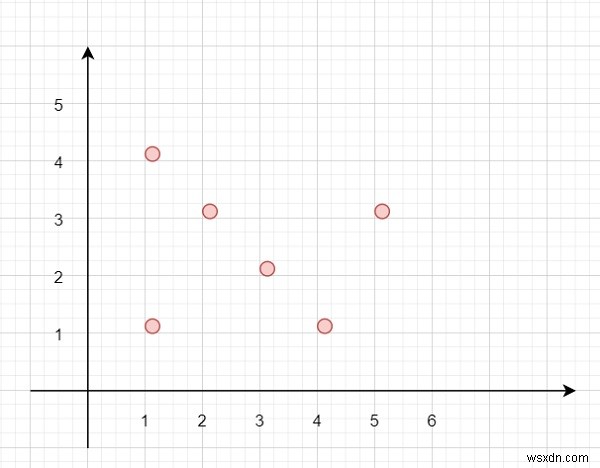
Sau đó, có 4 điểm

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• n:=số điểm, nếu n <3, thì trả về n

• ans:=2

• cho tôi trong phạm vi từ 1 đến n - 1

  • đếm:=0

  • lấy hai điểm từ chỉ số i và i - 1, đây là p1, p2

  • nếu điểm p1 và p2 giống nhau thì

    • cho j trong phạm vi 0 đến n - 1

      • nếu điểm [j] .x =p1.x và điểm [j] .y =p1.y, thì tăng số lượng lên 1

  • mặt khác -

    • cho j trong phạm vi 0 đến n - 1

      • p3:=điểm từ chỉ mục j

      • nếu p3.y - p2.y * p2.x - p1.x =p2.y - p1.y * p3.x - p2.x, thì hãy tăng số lượng lên 1

  • ans:=max of ans and count

• trả lại ans

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
class Solution {
   public:
   int maxPoints(vector<vector<int>>& points) {
      int n = points.size();
      if(n<3)return n;
      int ans = 2;
      for(int i = 1;i<n;i++){
         int count = 0;
         lli x1 = points[i-1][0];
         lli x2 = points[i][0];
         lli y1 = points[i-1][1];
         lli y2 = points[i][1];
         if(x1 == x2 && y1 == y2){
            for(int j =0;j<n;j++){
               if(points[j][0] ==x1 && points[j][1] == y1)count++;
            }
         } else {
            for(int j =0;j<n;j++){
               int x3 = points[j][0];
               int y3 = points[j][1];
               if((y3-y2)*(x2-x1) == (y2-y1)*(x3-x2))count++ ;
            }
         }
         ans = max(ans, count);
      }
      return ans;
   }
};
main(){
   Solution ob;
   vector<vector<int>> v = {{1,1},{3,2},{5,3},{4,1},{2,3},{1,4}};
   cout << (ob.maxPoints(v));
}

Đầu vào

[{1,1},{3,2},{5,3},{4,1},{2,3},{1,5}]

Đầu ra

4