BST hay cây tìm kiếm nhị phân là một dạng cây nhị phân có tất cả các nút bên trái nhỏ hơn và tất cả các nút bên phải lớn hơn giá trị gốc. Đối với vấn đề này, chúng tôi sẽ lấy một cây nhị phân và thêm tất cả các giá trị lớn hơn nút hiện tại vào nó. vấn đề "thêm tất cả các giá trị lớn hơn vào mọi nút trong BST" được đơn giản hóa vì đối với một BST, hãy thêm tất cả các giá trị nút lớn hơn giá trị nút hiện tại vào giá trị nút đó.
Thêm tất cả các giá trị lớn hơn vào mỗi nút trong Tuyên bố vấn đề BST -
Với Cây tìm kiếm nhị phân (BST), chúng ta cần thêm vào mỗi nút, tổng của tất cả các nút có giá trị lớn hơn.
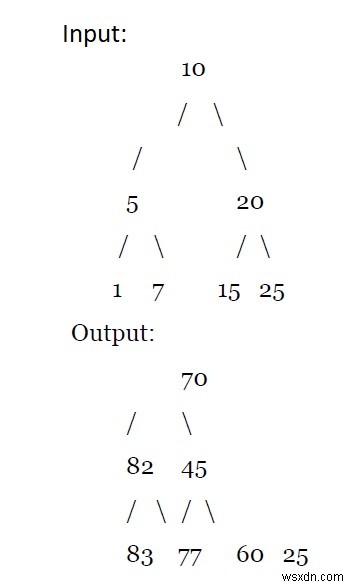
Giải thích
Chương trình này sẽ chuyển đổi một BST thành Cây nhị phân với giá trị của các nút là tổng của tất cả các phần tử lớn hơn cộng với giá trị ban đầu của nút.
Thêm tất cả các giá trị lớn hơn vào mỗi nút trong giải pháp Cây tìm kiếm nhị phân -
Chúng tôi sử dụng Reverse Inorder Traversal (đệ quy được gọi trên cây con bên phải trước tiên thay vì cây con bên trái) và duy trì một biến để lưu trữ tổng các nút đã được duyệt cho đến nay.
Sau đó, chúng tôi sử dụng tổng này để sửa đổi giá trị của nút hiện tại, bằng cách trước tiên cộng giá trị của nó vào tổng, sau đó thay thế giá trị của nút bằng tổng này.
Ví dụ
#include <iostream >
using namespace std;
struct node{
int data;
node *left;
node *right;
};
node *newNode(int key){
node *temp=new node;
temp->left=NULL;
temp->right=NULL;
temp->data=key;
return temp;
}
void Inorder(node *root){
if(!root)
return;
Inorder(root->left);
cout<<root->data<<" ";
Inorder(root->right);
}
node *Insert(node *root,int key){
if(!root)
return newNode(key);
if(key<root->data)
root->left=Insert(root->left,key);
else
root->right=Insert(root->right,key);
return root;
}
void RevInorderAdd(node *root,int &sum){
if(!root)
return;
RevInorderAdd(root->right,sum);
sum+=root->data;
root->data=sum;
RevInorderAdd(root->left,sum);
}
void AddGreater(node *root){
int sum=0;
RevInorderAdd(root,sum);
}
int main() {
/* Let us create following BST
10
/ \
5 20
/ \ / \
1 7 15 25 */
node *root = NULL;
root = Insert(root, 10);
Insert(root, 20);
Insert(root, 25);
Insert(root, 15);
Insert(root, 5);
Insert(root, 7);
Insert(root, 1);
Inorder(root);
cout<<endl;
AddGreater(root);
Inorder(root);
cout<<endl;
return 0;
} 