Thêm tất cả các giá trị lớn hơn vào mọi nút trong BST đã cho

Ở đây chúng ta sẽ thấy một vấn đề thú vị, nơi chúng ta sẽ thêm các giá trị lớn hơn vào mọi nút trong một cây tìm kiếm nhị phân nhất định. Vì vậy, cây đầu tiên và cây cuối cùng sẽ giống như bên dưới -

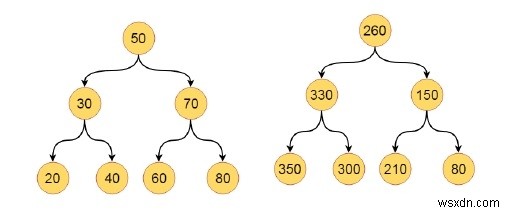
Thuật toán

bstUpdate (root, sum) -

Begin
   if root is null, then stop
   bstUpdate(right of room, sum)
   sum := sum + value of root
   update root value using sum
   bstUpdate(left of room, sum)
End

Ví dụ

#include<iostream>
using namespace std;
class Node {
   public:
      int data;
      Node *left, *right;
   };
   Node *getNode(int item) {
      Node *newNode = new Node();
      newNode->data = item;
      newNode->left = newNode->right = NULL;
      return newNode;
}
void updateBST(Node *root, int *sum) {
   if (root == NULL)
      return;
   updateBST(root->right, sum); //update right sub tree
   *sum = *sum + root->data;
   root->data = *sum; //update root data
   updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
   int sum = 0;
   updateBST(root, &sum);
}
void inorder(Node *root) {
   if (root != NULL) {
      inorder(root->left);
      cout<<root->data<<" ";
      inorder(root->right);
   }
}
Node* insert(Node* node, int data) {
   if (node == NULL)
      return getNode(data);
   if (data <= node->data) //go to left
      node->left = insert(node->left, data);
   else //go to right
      node->right = insert(node->right, data);
   return node;
}
int main() {
   int data[] = {50, 30, 20, 40, 70, 60, 80};
   int n = sizeof(data)/sizeof(data[0]);
   Node *root = NULL;
   for(int i = 0; i < n; i++) {
      root = insert(root, data[i]);
   }
   BSTUpdate(root);
   inorder(root);
}

Đầu ra

350 330 300 260 210 150 80