Giả sử chúng ta có một đồ thị vô hướng và một tập các đỉnh; chúng ta phải tìm tất cả các nút có thể truy cập từ mọi đỉnh có trong tập hợp đã cho.
Vì vậy, nếu đầu vào giống như
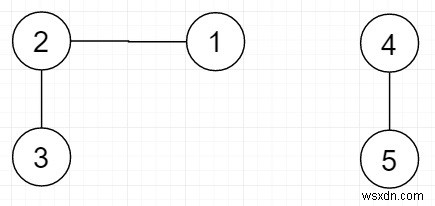
thì đầu ra sẽ là [1,2,3] và [4,5] vì đây là hai thành phần được kết nối.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- các nút:=số lượng các nút trong biểu đồ
- Xác định một mảng được truy cập có kích thước:các nút + 1. Và điền bằng 0
- Xác định một bản đồ m
- comp_sum:=0
- để khởi tạo i:=0, khi i
- u:=arr [i]
- nếu đã thăm [u] là sai, thì -
- (tăng comp_sum lên 1)
- m [đã thăm [u]]:=bfs truyền tải g từ nút u, cũng tính toán comp_sum
- in truyền tải của m [đã truy cập [u]]
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
class Graph{
public:
int nodes;
list<int> *adj_list;
Graph(int);
void insert_edge(int, int);
vector<int> BFS(int, int, int []);
};
Graph::Graph(int nodes) {
this->nodes = nodes;
adj_list = new list<int>[nodes+1];
}
void Graph::insert_edge(int u, int v) {
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
vector<int> Graph::BFS(int comp_sum, int src,int visited[]){
queue<int> queue;
queue.push(src);
visited[src] = comp_sum;
vector<int> reachableNodes;
while(!queue.empty()) {
int u = queue.front();
queue.pop();
reachableNodes.push_back(u);
for (auto itr = adj_list[u].begin(); itr != adj_list[u].end(); itr++) {
if (!visited[*itr]) {
visited[*itr] = comp_sum;
queue.push(*itr);
}
}
}
return reachableNodes;
}
void displayReachableNodes(int n, unordered_map <int, vector<int> > m) {
vector<int> temp = m[n];
for (int i=0; i<temp.size(); i++)
cout << temp[i] << " ";
cout << endl;
}
void get_all_reachable(Graph g, int arr[], int n) {
int nodes = g.nodes;
int visited[nodes+1];
memset(visited, 0, sizeof(visited));
unordered_map <int, vector<int> > m;
int comp_sum = 0;
for (int i = 0 ; i < n ; i++) {
int u = arr[i];
if (!visited[u]) {
comp_sum++;
m[visited[u]] = g.BFS(comp_sum, u, visited);
}
cout << "Reachable Nodes from " << u <<" are\n";
displayReachableNodes(visited[u], m);
}
}
int main() {
int nodes = 5;
Graph g(nodes);
g.insert_edge(1, 2);
g.insert_edge(2, 3);
g.insert_edge(4, 5);
int arr[] = {2, 4, 1};
int n = sizeof(arr)/sizeof(int);
get_all_reachable(g, arr, n);
} Đầu vào
g.insert_edge(1, 2); g.insert_edge(2, 3); g.insert_edge(4, 5);
Đầu ra
Reachable Nodes from 2 are 2 1 3 Reachable Nodes from 4 are 4 5 Reachable Nodes from 1 are 2 1 3
