Pizza với 3n lát trong C ++

Giả sử có một chiếc bánh pizza có 3n lát bánh to nhỏ khác nhau, em và hai người bạn sẽ lấy những lát bánh pizza như sau -

Tôi sẽ chọn bất kỳ lát bánh pizza nào.
Bạn của tôi, Amal sẽ chọn lát tiếp theo theo hướng ngược chiều kim đồng hồ với lựa chọn của tôi.
Bạn của tôi, Bimal sẽ chọn lát tiếp theo theo chiều kim đồng hồ của lựa chọn của tôi.
Lặp lại các bước này cho đến khi không còn lát pizza nào nữa.

Kích thước của lát Pizza được thể hiện bằng các lát mảng tròn theo chiều kim đồng hồ. Chúng tôi phải tìm tổng số kích thước lát cắt tối đa mà tôi có thể có.

Vì vậy, nếu đầu vào là [9,8,6,1,1,8],

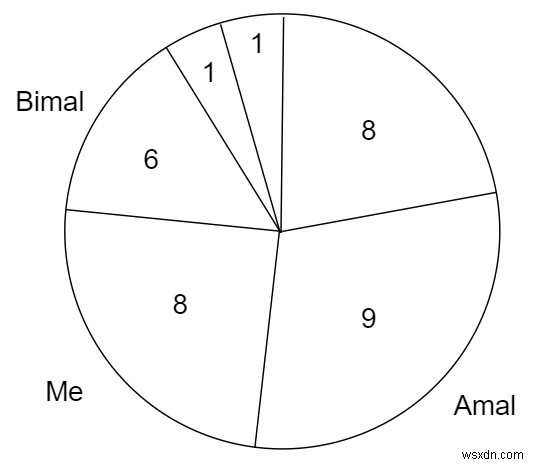
thì đầu ra sẽ là 16, mỗi lượt chọn lát bánh pizza có kích thước 8. Nếu tôi chọn lát có kích thước 9, bạn bè của tôi sẽ chọn lát có kích thước 8.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

Xác định một hàm giải quyết (), điều này sẽ nhận một mảng v và một đối số m,

n:=kích thước của v
Xác định hai mảng 2D dp1 và dp2 có kích thước (n + 1) x (m + 1) mỗi mảng
để khởi tạo i:=0, khi i
- để khởi tạo j:=0, khi j <=m, cập nhật (tăng j lên 1), thực hiện -
  - x:=v [i]
  - nếu j
    - dp2 [i + 1, j + 1] =tối đa của dp2 [i + 1, j + 1] và dp1 [i, j] + x)
    - dp1 [i + 1, j] =tối đa của dp1 [i + 1, j], dp2 [i, j] và dp1 [i, j]
trả về tối đa dp1 [n, m] và dp2 [n, m]
Từ phương thức chính, hãy làm như sau -
n:=kích thước của lát
ret:=0
ret:=tối đa của giải (các phần từ chỉ mục 1 đến cuối, n / 3) và các lát [0] + giải (các phần từ chỉ mục 2 đến cuối - 1, n / 3 - 1)
trả lại ret

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include <bits/stdc++.h>
using namespace std;
class Solution {
   public:
   int solve(vector <int> v, int m){
      int n = v.size();
      vector<vector<int> > dp1(n + 1, vector<int>(m + 1));
      vector<vector<int> > dp2(n + 1, vector<int>(m + 1));
      for (int i = 0; i < n; i++) {
         for (int j = 0; j <= m; j++) {
            int x = v[i];
            if (j < m)
            dp2[i + 1][j + 1] = max(dp2[i + 1][j + 1], dp1[i]
            [j] + x);
            dp1[i + 1][j] = max({ dp1[i + 1][j], dp2[i][j],
            dp1[i][j] });
         }
      }
      return max(dp1[n][m], dp2[n][m]);
   }
   int maxSizeSlices(vector<int>& slices) {
      int n = slices.size();
      int ret = 0;
      ret = max(solve(vector<int>(slices.begin() + 1,
      slices.end()), n / 3), slices[0] + solve(vector<int>(slices.begin() +
      2, slices.end() - 1), n / 3 - 1));
      return ret;
   }
};
main(){
   Solution ob;
   vector<int> v = {9,8,6,1,1,8};
   cout << (ob.maxSizeSlices(v));
}

Đầu vào

{9,8,6,1,1,8}

Pizza với 3n lát trong C ++

Ví dụ

Đầu vào

Đầu ra