Chương trình cho số không theo tiêu chí trung tâm trong C ++

Số phi mùa ở giữa chứa các lớp phi mùa được tạo thành bởi các dấu chấm và một dấu chấm tương ứng ở trung tâm.

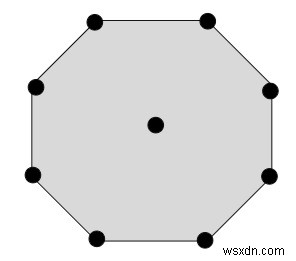
Ở trên là con số của số không có tâm 𝑁2. Nó có thể được tính bằng công thức -

$$ Nc (n) =\ frac {(3n-2) (3n-1)} {2} $$

Đầu vào

number: 20

Đầu ra

centered nonagonal number : 1711

Đầu vào

number: 10

Đầu ra

centered nonagonal series : 1 10 28 55 91 136 190 253 325 406

Thuật toán

Start
Step 1→ declare function to calculate centered nonagonal number
   int calculate_number(int num)
      return (3 * num - 2) * (3 * num - 1) / 2
Step 2→ declare function to calculate centered nonagonal series
   int calculate_series(int num)
      Loop For int i = 1and i <= num and i++
         Print (3 * i - 2) * (3 * i - 1) / 2
      End
Step 3→ In main()
   Declare int num = 20
   Call calculate_number(num)
   Declare num = 10
   Call calculate_series(num)
Stop

Ví dụ

#include <bits/stdc++.h>
using namespace std;
//calculate centered nonagonal number
int calculate_number(int num){
   return (3 * num - 2) * (3 * num - 1) / 2;
}
int calculate_series(int num){
   for (int i = 1; i <= num; i++){
      cout << (3 * i - 2) * (3 * i - 1) / 2;
      cout << " ";
   }
}
int main(){
   int num = 20;
   cout<<"centered nonagonal number : "<<calculate_number(num)<<endl;
   num = 10;
   cout<<"centered nonagonal series : ";
   calculate_series(num);
   return 0;
}

Đầu ra

Nếu chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -

centered nonagonal number : 1711
centered nonagonal series : 1 10 28 55 91 136 190 253 325 406