Số Catalan là một dãy số. Các số Catalan tạo thành một chuỗi các số tự nhiên xuất hiện trong các bài toán đếm khác nhau, thường liên quan đến các đối tượng được xác định đệ quy.
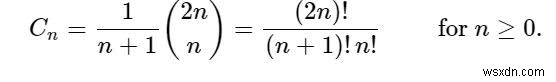
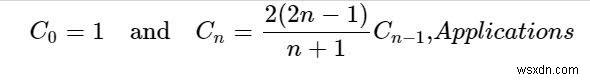
-
C n là số từ Dyck có độ dài 2n. Một từ Dyck là một chuỗi bao gồm n X và n Y sao cho không đoạn ban đầu của chuỗi có nhiều Y hơn X. Ví dụ:sau đây là các từ Dyck có độ dài 6
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.
-
Diễn giải lại ký hiệu X là dấu ngoặc đơn mở và Y là dấu ngoặc đơn đóng, C n đếm số lượng biểu thức chứa n cặp dấu ngoặc đơn được khớp chính xác
((())) ()(()) ()()() (())() (()())
-
C n là số cách khác nhau n + 1 thừa số có thể hoàn toàn nằm trong ngoặc đơn (hoặc số cách kết hợp n ứng dụng của một toán tử nhị phân). Ví dụ:đối với n =3, chúng ta có năm dấu ngoặc đơn khác nhau gồm bốn yếu tố sau:
((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))
-
Các ứng dụng kế tiếp của toán tử nhị phân có thể được biểu diễn dưới dạng cây nhị phân đầy đủ. (Một cây nhị phân gốc sẽ đầy nếu mọi đỉnh có hai con hoặc không con.) Sau đó C n là số cây nhị phân đầy đủ có n + 1 lá:
Mẫu
Đầu vào - 6
Đầu ra - 1 1 2 5 14 42
Giải thích
Các số Catalan đầu tiên cho n =0, 1, 2, 3,4,5,6,7,8,9,10, ... là
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
Ví dụ
#include<iostream>
using namespace std;
long int catalan( int n) {
if (n <= 1){
return 1;
}
long int result = 0;
for (int i=0; i<n; i++){
result += catalan(i)*catalan(n-i-1);
}
return result;
}
int main(){
for (int i=0; i<6; i++)
cout << catalan(i) << " ";
return 0;
} Đầu ra
1 1 2 5 14 42
