Trong bài toán này, chúng ta được cung cấp một cây nhị phân và chúng ta được cung cấp các truy vấn Q. Ourtask là tạo một chương trình để giải quyết các Truy vấn để tìm khoảng cách giữa hai nút của một cây nhị phân - phương thức O (logn) trong C ++.
Mô tả vấn đề
Trong mỗi truy vấn, chúng ta được cung cấp hai nút của cây nhị phân và chúng ta cần tìm khoảng cách số giữa hai nút, tức là số cạnh được duyệt để đến một nút từ một nút khác.
Hãy lấy một ví dụ để hiểu vấn đề,
Đầu vào :Cây nhị phân
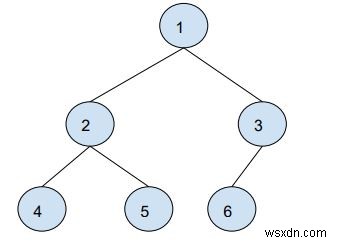
Truy vấn =3
Q1 -> [2, 6]
Quý 2 -> [4, 1]
Q3 -> [5, 3]
Đầu ra: 3, 2, 3
Phương pháp tiếp cận giải pháp
Để giải quyết vấn đề, chúng tôi sẽ sử dụng công thức khoảng cách sử dụng tổ tiên chung thấp nhất (LCA) và khoảng cách của chúng.
Khoảng cách (n1, n2) =khoảng cách (gốc, n1) + khoảng cách (gốc, n1) - 2 * khoảng cách (gốc, LCA)
Để giải quyết vấn đề sẽ làm theo các bước sau,
-
Tìm cấp độ của mỗi nút, tức là N1, N2, LCA.
-
Sau đó, chúng tôi sẽ tìm các mảng của cây nhị phân dựa trên cây Tourof của Euler.
-
Sau đó, chúng tôi sẽ tạo một cây phân đoạn cho LCA.
Ví dụ
#include <bits/stdc++.h>
#define MAX 1000
using namespace std;
int eulerArray[MAX];
int eIndex = 0;
int vis[MAX];
int L[MAX];
int H[MAX];
int level[MAX];
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data) {
struct Node* temp = new struct Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void FindNodeLevels(struct Node* root) {
if (!root)
return;
queue<pair<struct Node*, int> > q;
q.push({ root, 0 });
pair<struct Node*, int> p;
while (!q.empty()) {
p = q.front();
q.pop();
level[p.first->data] = p.second;
if (p.first->left)
q.push({ p.first->left, p.second + 1 });
if (p.first->right)
q.push({ p.first->right, p.second + 1 });
}
}
void createEulerTree(struct Node* root) {
eulerArray[++eIndex] = root->data;
if (root->left) {
createEulerTree(root->left);
eulerArray[++eIndex] = root->data;
}
if (root->right) {
createEulerTree(root->right);
eulerArray[++eIndex] = root->data;
}
}
void creareEulerArray(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[eulerArray[i]];
if (vis[eulerArray[i]] == 0) {
H[eulerArray[i]] = i;
vis[eulerArray[i]] = 1;
}
}
}
pair<int, int> seg[4 * MAX];
pair<int, int> min(pair<int, int> a, pair<int, int> b) {
if (a.first <= b.first)
return a;
else
return b;
}
pair<int, int> buildSegTree(int low, int high, int pos) {
if (low == high) {
seg[pos].first = L[low];
seg[pos].second = low;
return seg[pos];
}
int mid = low + (high - low) / 2;
buildSegTree(low, mid, 2 * pos);
buildSegTree(mid + 1, high, 2 * pos + 1);
seg[pos] = min(seg[2 * pos], seg[2 * pos + 1]);
}
pair<int, int> LCA(int qlow, int qhigh, int low, int high, int pos) {
if (qlow <= low && qhigh >= high)
return seg[pos];
if (qlow > high || qhigh < low)
return { INT_MAX, 0 };
int mid = low + (high - low) / 2;
return min(LCA(qlow, qhigh, low, mid, 2 * pos), LCA(qlow, qhigh,mid + 1, high, 2 * pos +1));
}
int CalcNodeDistance(int node1, int node2, int size) {
int prevn1 = node1, prevn2 = node2;
node1 = H[node1];
node2 = H[node2];
if (node2 < node1)
swap(node1, node2);
int lca = LCA(node1, node2, 1, size, 1).second;
lca = eulerArray[lca];
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
int main() {
int N = 6;
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
FindNodeLevels(root);
createEulerTree(root);
creareEulerArray(2 * N - 1);
buildSegTree(1, 2 * N - 1, 1);
int Q = 4;
int query[Q][2] = {{1, 5}, {4, 6}, {3, 4}, {2, 4} };
for(int i = 0; i < Q; i++)
cout<<"The distance between two nodes of binary tree is "<<CalcNodeDistance(query[i][0], query[i][1], 2 * N - 1)<<endl;
return 0;
} Đầu ra
The distance between two nodes of binary tree is 2 The distance between two nodes of binary tree is 4 The distance between two nodes of binary tree is 3 The distance between two nodes of binary tree is 1
