Chúng tôi được cung cấp với một cây nhị phân gồm các nút riêng biệt và hai nút của cây nhị phân có đường dẫn trong cây nhị phân mà chúng tôi muốn in.
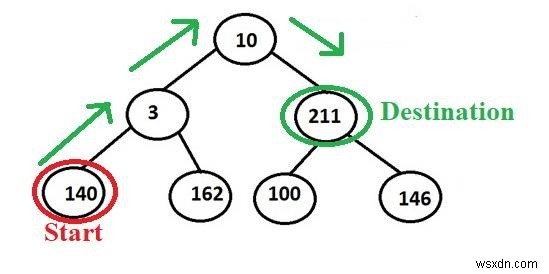
Ví dụ - Chúng tôi muốn in đường dẫn giữa nút 140 đến 211 vì vậy đầu ra của nó sẽ giống như -
Output: 140->3->10->211
Ý tưởng là tìm các đường dẫn tạo thành các nút gốc đến hai nút và lưu trữ chúng trong hai vectơ hoặc mảng riêng biệt như path1 và path2.
Bây giờ, có hai trường hợp khác nhau -
- Nếu hai nút nằm trong các cây con khác nhau của các nút gốc - Khi hai nút ở các cây con khác nhau như nút ở bên trái và nút ở bên phải. Trong trường hợp này, rõ ràng là nút gốc sẽ nằm giữa đường dẫn từ nút1 đến nút2. Vì vậy, hãy in path1 theo thứ tự ngược lại rồi đến path2.
-
Nếu các nút nằm trong cùng một cây con - Khi cả hai nút nằm trong cùng một cây con có thể nằm trong cây con bên trái hoặc trong cây con bên phải. Trong trường hợp này, bạn cần quan sát đường đi từ gốc đến hai nút sẽ có điểm giao nhau mà trước đó đường đi là chung cho cả hai nút từ nút gốc. Chúng ta phải tìm giao điểm và in các nút từ điểm đó như trường hợp trên.
Thuật toán
START STEP 1-> DEFINE A struct Node WITH int data AND Node *left, *right; STEP 2-> DEFINE A TREE STRUCTURE struct Node* tree(int data)FUNCTION bool path(Node* root, vector& arr, int x) STEP 1-> IF root IS NULL RETURN false END IF STEP 2-> arr.push_back(root->data) IF root->data == x THEN RETURN true END IF STEP 3-> IF path(root->left, arr, x) || path(root->right, arr, x) THEN, RETURN true STEP 4-> arr.pop_back() return false END FUNCTION FUNCTION void printPath(Node* root, int n1, int n2) STEP 1-> DEFINE A vector<int> path1 STEP 2-> DEFINE A vector<int> path2 STEP 3-> CALL FUNCTION path(root, path1, n1) STEP 4-> CALL FUNCTION path(root, path2, n2) STEP 5-> DEFINE AND SET intersection = -1, i = 0, j = 0 STEP 6-> LOOP WHILE i != path1.size() || j != path2.size() IF i == j && path1[i] == path2[j] INCREMENT i BY 1 INCREMENT j BY 1 ELSE SET intersection = j - 1 BREAK; END IF END WHILE STEP 7-> LOOP FOR i = path1.size() – 1 AND i > intersection AND i--PRINT path1[i] END FOR STEP 8-> LOOP FOR i = intersection AND i < path2.size() AND i++ PRINT path2[i] END FOR
Ví dụ
#include <bits/stdc++.h>
using namespace std;
// structure of a node of binary tree
struct Node {
int data;
Node *left, *right;
};
struct Node* tree(int data){
struct Node* newNode = new Node;
newNode->data = data;
newNode->left = newNode->right = NULL;
return newNode;
}
bool path(Node* root, vector<int>& arr, int x){
if (!root)
return false;
// push the node's value in 'arr'
arr.push_back(root->data);
// if it is the required node
// return true
if (root->data == x)
return true;
if (path(root->left, arr, x) || path(root->right, arr, x))
return true;
arr.pop_back();
return false;
}
// Function to print the path between
// any two nodes in a binary tree
void printPath(Node* root, int n1, int n2){
// vector to store the path
vector<int> path1;
vector<int> path2;
path(root, path1, n1);
path(root, path2, n2);
int intersection = -1;
int i = 0, j = 0;
while (i != path1.size() || j != path2.size()) {
if (i == j && path1[i] == path2[j]) {
i++;
j++;
} else {
intersection = j - 1;
break;
}
}
// Print the required path
for (int i = path1.size() - 1; i > intersection; i--)
cout << path1[i] << " ";
for (int i = intersection; i < path2.size(); i++)
cout << path2[i] << " ";
}
int main(){
// binary tree formation
struct Node* root = tree(1);
root->left = tree(2);
root->left->left = tree(4);
root->left->left->left = tree(6);
root->left->right = tree(5);
root->left->right->left = tree(7);
root->left->right->right = tree(8);
root->right = tree(3);
root->right->left = tree(9);
root->right->right = tree(10);
int node1 = 5;
int node2 = 9;
printPath(root, node1, node2);
return 0;
} Đầu ra
Chương trình này sẽ in đầu ra -
5 2 1 3 9
