Đếm số lượng hình thoi có thể có bên trong một hình chữ nhật có kích thước nhất định trong C ++

Chúng tôi được cung cấp một hình chữ nhật với kích thước là chiều cao X chiều rộng. Hình chữ nhật được biểu diễn trên hệ tọa độ 2D với góc dưới bên trái tại điểm (0,0). Vì vậy, mục tiêu là đếm số lượng hình thoi có thể có bên trong hình chữ nhật này sao cho tất cả các điều kiện này được đáp ứng -

• Hình thoi có diện tích hơn 0.

• Các đường chéo của hình thoi song song với trục x và y.

• Hình thoi có tọa độ nguyên cho tất cả các góc.

Hãy cho chúng tôi hiểu với các ví dụ

Đầu vào - chiều dài =3 chiều rộng =3

Đầu ra - Đếm số hình thoi có thể có bên trong một hình chữ nhật có kích thước cho trước là:4

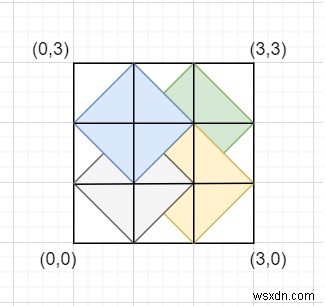
Giải thích - Hình bên dưới có một hình chữ nhật chiều cao =chiều rộng =3. Ngoài ra, chúng ta có thể thấy bốn hình thoi có diện tích> 0 và các đường chéo song song với cả hai trục (cũng là tọa độ nguyên) -

First [ (1,0), (2,1), (1,2), (0,1) ]
Second [ (2,0), (3,1), (2,2), (1,1) ]
Third [ (2,1), (3,2), (2,3), (1,2) ]
Fourth [ (1,1), (2,1), (1,2), (0,1) ]

Đầu vào - chiều dài =2 chiều rộng =3

Đầu ra - Số lượng hình thoi có thể có bên trong một hình chữ nhật có kích thước cho trước là:2

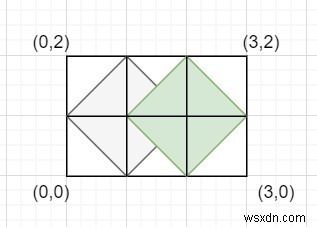
Giải thích - Hình bên dưới có một hình chữ nhật chiều cao =2 chiều rộng =3. Ngoài ra, chúng ta có thể thấy hai hình thoi bên trong

Cách tiếp cận được sử dụng trong chương trình dưới đây như sau

Hình thoi đầu tiên có diện tích khác 0 và tọa độ nguyên sẽ bắt đầu từ góc trên bên phải tại (2,2). Bắt đầu duyệt từ các chỉ mục i =j =2 đến i <=length và j <=length. Tăng i và j lên 2 để cố định độ dài chẵn (đối với tọa độ nguyên). Số lượng hình thoi có các đường chéo này sẽ là (chiều cao-i + 1) X (chiều rộng-j + 1).

• Lấy chiều dài và chiều rộng làm số nguyên.

• Hàm could_rhombus (int length, int width) nhận kích thước của một hình chữ nhật và trả về số lượng hình thoi có thể có bên trong hình chữ nhật tuân theo tất cả các điều kiện đã đề cập.

• Lấy số lượng ban đầu là 0.

• Đi ngang từ i =2 đến i <=length và j =2 đến j <=width.

• Với mỗi i, j lấy temp_1 =length-i + 1 và temp_2 =width-j + 1

• Thêm temp_1 * temp_2 để đếm.

• Tăng i và j lên 2 (đối với tọa độ nguyên).

• Kết quả là số lượt trả lại ở cuối.

Ví dụ

#include <bits/stdc++.h>
using namespace std;
long long possible_rhombus(int height, int width){
   long long count = 0;
   for (int i = 2; i <= height; i += 2){
      for (int j = 2; j <= width; j += 2){
         int temp_1 = height - i + 1;
         int temp_2 = width - j + 1;
         count += temp_1 * temp_2;
      }
   }
   return count;
}
int main(){
   int height = 4, width = 4;
   cout<<"Count of number of rhombi possible inside a rectangle of given size are: "<<possible_rhombus(height, width);
   return 0;
}

Đầu ra

Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -

Count of number of rhombi possible inside a rectangle of given size are: 16