Đếm số ô vuông trong một hình chữ nhật trong C ++

Chúng tôi cho một hình chữ nhật có chiều dài L và chiều rộng B, sao cho L> =B. Mục tiêu là tìm số ô vuông mà một hình chữ nhật có kích thước LXB có thể chứa được.

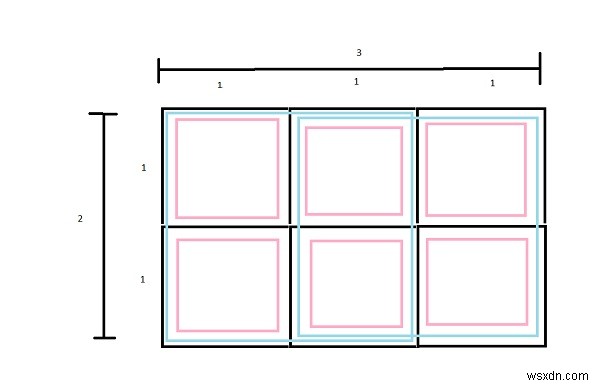
Hình trên cho thấy một hình chữ nhật có kích thước 3 X 2. Nó có các hình vuông 2, 2X2 và 6,1X1.

Tổng số ô vuông =6 + 2 =8.

Mỗi hình chữ nhật có kích thước LXB đều có số ô vuông 1X1 L * B.
Hình vuông lớn nhất có kích thước BXB.
Đối với L =B =1, bình phương =1.
Đối với L =B =2, bình phương =1 + 4 =5. (1 của 2X2, 4 của 1X1)
Đối với L =B =3, bình phương =1 + 4 + 9 =14. (1 của 3X3, 4 của 2X2, 9 của 1X1)
Đối với L =B =4, hình vuông =1 + 4 + 9 + 16 =30 (1 của 4X4, 4 của 3X3, 9 của 2X2, 16 của 1X1)
…………… ..
Đối với mỗi hình chữ nhật BXB số ô vuông là

for ( i=1 to B )
No. of squares + = i*i.

Khi L> B. Nhiều hình vuông sẽ được thêm vào. Khi L =B + 1 (thừa 1 cột so với B). Khi đó các ô vuông được thêm vào sẽ là L + (L-1) +…. + 3 + 2 + 1 =L (L + 1) / 2

Vì vậy, đối với các cột L-B bổ sung, các hình vuông được thêm vào sẽ là (L-B) * (B) (B + 1) / 2

Tổng số hình vuông sẽ là hình vuông theo BXB + (L-B) * (L) (L + 1) / 2.
Bạn cũng có thể sử dụng công thức B (B + 1) (2B + 1) / 6 cho chuỗi (1 + 4 + 9 + ...... BXB) trong bước 8.

Hãy cùng hiểu với các ví dụ.

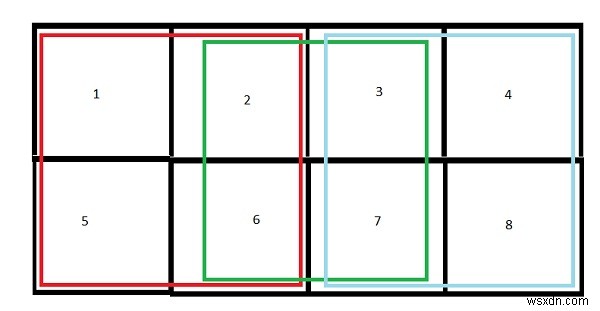
Đầu vào - L =4, B =2

Đầu ra - Số ô vuông trong hình chữ nhật - 11

Giải thích - 8 hình vuông của 1X1 và 3 của 2X2.

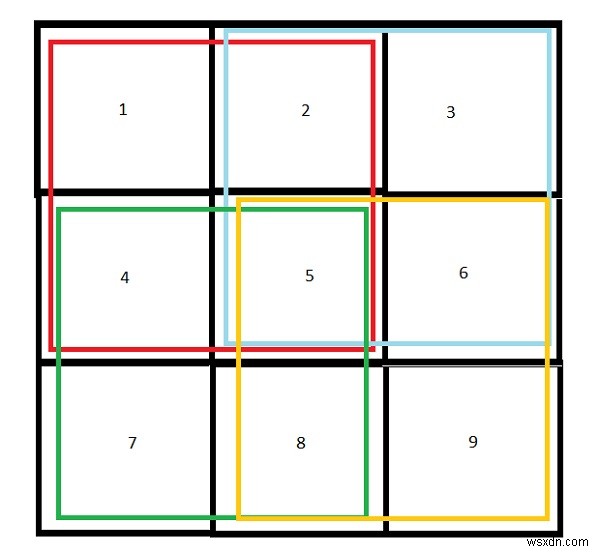
Đếm số ô vuông trong một hình chữ nhật trong C ++

Đầu vào - L =3, B =3

Đầu ra - Số ô vuông trong hình chữ nhật - 14

Giải thích - 9 hình vuông của 1X1, 4 của 2X2 và 1 của 3X3.

Đếm số ô vuông trong một hình chữ nhật trong C ++

Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau

Chúng tôi lấy chiều dài và chiều rộng số nguyên cho kích thước của hình chữ nhật.
Hàm numofSquares (int l, int b) nhận kích thước và trả về số ô vuông trong hình chữ nhật có kích thước lXb.
Đối với hình vuông lớn nhất bXb. Sử dụng vòng lặp for từ 1 đến b và thêm từng i * i vào các ô vuông.
Bây giờ nếu l> b. Các ô vuông mới được thêm vào sẽ là (l-b) (b) (b + 1) / 2. Thêm cái này vào hình vuông.
Trả về các ô vuông như kết quả mong muốn.

Lưu ý - giữ chiều dài> =chiều rộng

Ví dụ

#include<iostream>
using namespace std;
int numofSquares(int l, int b){
   int squares=0;
   for(int i=1;i<=b;i++) //squares inside biggest square of size breadth X breadth{
      squares += i*i;
   }
   squares+=(l-b)*b*(b+1)/2;
   return squares;
}
int main(){
   int length = 5, breadth = 4; //keep length always >= breadth
   cout << "Count of squares is :"<< numofSquares(length,breadth);
}

Đầu ra

Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -

Count of squares is :40