Nó là một thuật toán nhân ma trận dựa trên chia và chinh phục phương pháp. Nó được sử dụng để nhân hai ma trận có cùng kích thước,
Tìm phép nhân của hai ma trận−
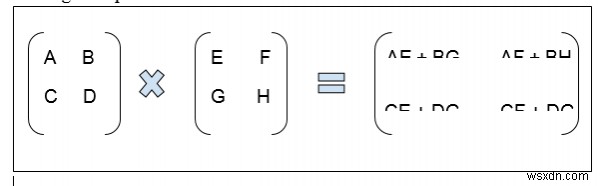
Thuật toán của strassen giảm chi phí cho phép nhân bằng cách đơn giản hóa phép nhân.
Đây là phép nhân được thực hiện bằng Thuật toán của strassen:
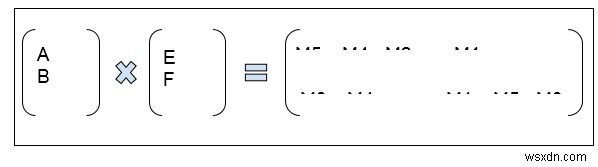
M1 =a * (f - h)
M2 =(a + b) * h
M3 =(c + d) * e
M4 =d * (g - e)
M5 =(a + d) * (e + h)
M6 =(b - d) * (g + h)
M7 =(a - c) * (e + f)
Điều này có thể dễ dàng ghi nhớ và mã thuật toán có thể được giải mã. Đối với điều này, chúng tôi có một số quy tắc, trước tiên hãy nhớ 6 điều này−
- Sử dụng AHED cho 4 giá trị đầu tiên của M.
- Sử dụng Phép nhân đường chéo cho giá trị thứ 5 của M.
- Sử dụng CR cuối cùng (cột cuối cùng từ thảm 1 và hàng cuối cùng ở mẫu 2) cho giá trị thứ 6 của M.
- Sử dụng CR đầu tiên (cột đầu tiên từ thảm 1 và hàng đầu tiên ở dạng 2) cho giá trị thứ 7 của M.
- Trong khi xem xét các phần tử của hàng, hãy thêm chúng và trong trường hợp các cột trừ chúng đi.
- Các giá trị cập nhật sau đó bằng cách sử dụng các giá trị liền kề.
Sử dụng những cách này, chúng tôi có thể dễ dàng ghi nhớ các giá trị.
