Ma trận xoắn ốc III trong C ++

Giả sử chúng ta có một lưới 2 chiều với R hàng và C cột, chúng ta bắt đầu từ (r0, c0) quay về hướng đông. Ở đây, góc tây bắc của lưới nằm ở hàng và cột đầu tiên và góc đông nam của lưới nằm ở hàng và cột cuối cùng. Chúng ta sẽ đi theo hình xoắn ốc theo chiều kim đồng hồ để thăm mọi vị trí trong lưới này. Khi chúng ta ở ngoài ranh giới của lưới, chúng ta tiếp tục đi bộ ra ngoài lưới (nhưng có thể quay trở lại ranh giới lưới sau đó.). Chúng ta phải tìm một danh sách các tọa độ đại diện cho các vị trí của lưới theo thứ tự mà chúng đã được truy cập. Vì vậy, nếu lưới giống như -

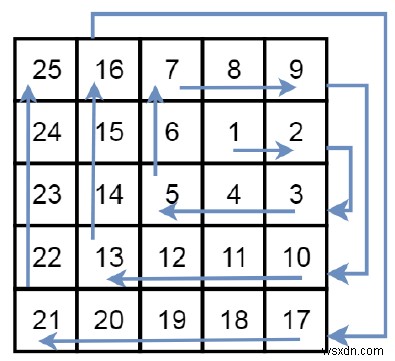
Sau đó, mũi tên sẽ là đường dẫn.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Tạo dirr:=[[0,1], [1,0], [0, -1], [- 1,0]]

• tạo ma trận ret, len:=0, dir:=0

• insert (r0, c0) vào ret

• trong khi kích thước của ret

  • nếu dir =0 hoặc dir =2, thì tăng len lên 1

  • cho tôi trong phạm vi từ 0 đến len - 1

    • r0:=r0 + dirr [dir, 0], c0:=c0 + dirr [dir, 1]

    • nếu r0 trong phạm vi từ 0 đến R và c0 trong phạm vi 0 đến C, thì hãy chuyển sang lần lặp tiếp theo

    • insert (r0, c0) vào ret

  • dir:=(dir + 1) mod 4

• trả lại ret

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<vector<auto> > v){
   cout << "[";
   for(int i = 0; i<v.size(); i++){
      cout << "[";
      for(int j = 0; j <v[i].size(); j++){
         cout << v[i][j] << ", ";
      }
      cout << "],";
   }
   cout << "]"<<endl;
}
int dirr[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
class Solution {
   public:
   vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
      vector < vector <int> > ret;
      int len = 0;
      int dir = 0;
      ret.push_back({r0, c0});
      while(ret.size() < R * C){
         if(dir == 0 || dir == 2) len++;
         for(int i = 0; i < len; i++){
            r0 = r0 + dirr[dir][0];
            c0 = c0 + dirr[dir][1];
            if(r0 < 0 || c0 < 0 || c0 >= C || r0 >= R) continue;
            ret.push_back({r0, c0});
         }
         dir = (dir + 1) % 4;
      }
      return ret;
   }
};
main(){
   Solution ob;
   print_vector(ob.spiralMatrixIII(5,5,1,3));
}

Đầu vào

5

5

1

3

Đầu ra

[[1,3],[1,4],[2,4],[2,3],[2,2],[1,2],[0,2],[0,3],[0,4],[3,4],[3,3],[3,2],[3,1],[2,1],[1,1],[0,1],[4,4],[4,3],[4,2],[4,1],[4,0],[3,0],[2,0],[1,0],[0,0]]