Trong bài toán này, chúng ta được đưa ra một ma trận 2D. Nhiệm vụ của chúng tôi là in tất cả các phần tử của ma trận theo thứ tự đường chéo.
Hãy lấy một ví dụ để hiểu vấn đề,
1 2 3 4 5 6 7 8 9
Đầu ra -
1 4 2 7 5 3 8 6 9
Hãy xem mẫu được theo sau khi in ma trận ở dạng ngoằn ngoèo hoặc dạng đường chéo.
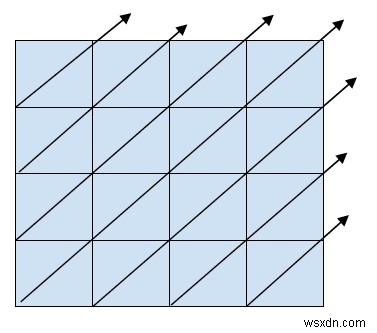
Đây là cách hoạt động của đường chéo.
Số dòng trong đầu ra luôn phụ thuộc vào hàng và cột của ma trận 2D.
Đối với mat ma trận 2D [r] [c], chúng sẽ là r + c-1 dòng đầu ra.
Ví dụ
Bây giờ, hãy xem giải pháp cho chương trình,
#include <iostream>
using namespace std;
#define R 5
#define C 4
int min2(int a, int b)
{ return (a < b)? a: b; }
int min3(int a, int b, int c)
{ return min2(min2(a, b), c);}
int max(int a, int b)
{ return (a > b)? a: b; }
void printDiagonalMatrix(int matrix[][C]){
for (int line=1; line<=(R + C -1); line++){
int start_col = max(0, line-R);
int count = min3(line, (C-start_col), R);
for (int j=0; j<count; j++)
cout<<matrix[min2(R, line)-j-1][start_col+j]<<"\t";
cout<<endl;
}
}
int main(){
int M[R][C] = {{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16},
{17, 18, 19, 20},};
cout<<"The matrix is : \n";
for (int i=0; i< R; i++){
for (int j=0; j<C; j++)
cout<<M[i][j]<<"\t";
cout<<endl;
}
cout<<"\nZigZag (diagnoal) traversal of matrix is :\n";
printDiagonalMatrix(M);
return 0;
} Đầu ra
The matrix is : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ZigZag (diagonal) traversal of matrix is : 1 5 2 9 6 3 13 10 7 4 17 14 11 8 18 15 12 19 16 20
