Chương trình tìm chi phí tối thiểu để kết nối mỗi tọa độ Descartes trong C ++

Giả sử chúng ta có một danh sách các điểm tọa độ Descartes 2D (x, y). Chúng ta có thể kết nối (x0, y0) và (x1, y1), có chi phí là | x0 - x1 | + | y0 - y1 |. Nếu chúng tôi được phép kết nối bất kỳ số điểm nào, chúng tôi phải tìm chi phí tối thiểu cần thiết để mọi điểm được kết nối bằng một đường dẫn.

Vì vậy, nếu đầu vào giống như điểm =[[0, 0], [0, 2], [0, -2], [2, 0], [- 2, 0], [2, 3], [2 , -3]],

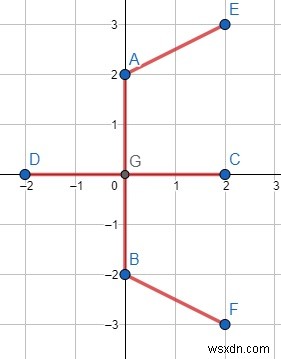
thì đầu ra sẽ là 14 vì, từ (0, 0) đến (0, 2), (0, -2), (2, 0), (- 2, 0), chi phí là 2, tổng là 8, và (2, 3) gần nhất với (0, 2), chi phí là | 2 + 1 | =3 và đối với (2, -3) nó gần nhất với (0, -2), chi phí cũng bằng 3. vì vậy tổng chi phí là 8 + 6 =14.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• MAX:=inf
• Xác định một khoảng hàm (), điều này sẽ lấy i, j và mảng điểm p,
• return | (p [i, x] - p [j, x]) + | p [i, y] - p [j, y] ||
• Từ phương pháp chính, hãy thực hiện như sau -
• n:=kích thước của p
• nếu n <2, thì:trả về 0
• Xác định một mảng được gọi là khoảng cách với n vị trí và điền bằng MAX
• Xác định một mảng được truy cập có kích thước n
• khoảng cách [0]:=0
• để khởi tạo i:=0, khi i
• min_d:=MAX
• nút:=0
• để khởi tạo j:=0, khi j
• nếu đã thăm [j] là false và khoảng cách [j]
• min_d:=distance [j]
• nút:=j

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <iostream>
#include <vector>
#define MAX 99999
using namespace std;

int interval(int i, int j, vector<vector<int>>& p) {
   return abs(p[i][0] - p[j][0]) + abs(p[i][1] - p[j][1]);
}

int solve(vector<vector<int>>& p) {
   int n = p.size(), cost = 0;
   if (n < 2) return 0;

   vector<int> distance(n, MAX);
   vector<bool> visited(n);

   distance[0] = 0;

   for (int i = 0; i < n; i++) {
      int min_d = MAX, node = 0;
      for (int j = 0; j < n; j++) {
         if (!visited[j] && distance[j] < min_d) {
            min_d = distance[j];
            node = j;
         }
      }

      visited[node] = true;
      cost += distance[node];

      for (int j = 0; j < n; j++) {
         if (!visited[j]) {
            int d = interval(node, j, p);
            distance[j] = min(distance[j], d);
         }
      }
   }
   return cost;
}

int main(){
   vector<vector<int>> points = {{0, 0},{0, 2},{0, -2},{2, 0},{-2, 0}, {2, 3}, {2, -3}};
cout << solve(points);
}

Đầu vào

{{0, 0},{0, 2},{0, -2},{2, 0},{-2, 0}, {2, 3}, {2, -3}}

Đầu ra

14