Hồi quy logistic là một kỹ thuật thống kê để dự đoán kết quả nhị phân. Đây không phải là một điều mới vì nó hiện đang được áp dụng trong các lĩnh vực từ tài chính đến y học đến tội phạm học và các ngành khoa học xã hội khác.
Trong phần này, chúng tôi sẽ phát triển hồi quy logistic bằng cách sử dụng python, mặc dù bạn có thể triển khai tương tự bằng các ngôn ngữ khác như R.
Cài đặt
Chúng tôi sẽ sử dụng các thư viện bên dưới trong chương trình mẫu của mình,
-
Khó chịu :Để xác định mảng số và ma trận
-
Gấu trúc :Để xử lý và vận hành trên dữ liệu
-
Mô hình thống kê :Để xử lý ước tính tham số &kiểm tra thống kê
-
Pylab :Để tạo các lô
Bạn có thể cài đặt các thư viện trên bằng cách sử dụng pip bằng cách chạy lệnh dưới đây trong CLI.
> pip cài đặt số liệu thống kê về gấu trúc numpy
Trường hợp sử dụng mẫu cho hồi quy logistic
Để kiểm tra hồi quy logistic của chúng tôi trong python, chúng tôi sẽ sử dụng dữ liệu hồi quy logit do UCLA (Viện nghiên cứu và giáo dục kỹ thuật số) cung cấp. Bạn có thể truy cập dữ liệu từ liên kết dưới đây ở định dạng csv: https://stats.idre.ucla.edu/stat/data/binary.csv
Tôi đã lưu tệp csv này trong máy cục bộ của mình và sẽ đọc dữ liệu từ đó, bạn có thể làm. Với tệp csv này, chúng tôi sẽ xác định các yếu tố khác nhau có thể ảnh hưởng đến việc nhập học vào trường cao học.
Nhập các thư viện bắt buộc và tải tập dữ liệu
Chúng tôi sẽ đọc dữ liệu bằng thư viện gấu trúc (pandas.read_csv):
import pandas as pdimport statsmodels.api as smimport pylab as plimport numpy as npdf =pd.read_csv ('binary.csv') # Chúng tôi có thể đọc dữ liệu trực tiếp từ liên kết \ # df =pd.read_csv ('https://stats.idre.ucla.edu/stat/data/binary.csv ') print (df.head ()) Đầu ra
thừa nhận gre gpa rank0 0 380 3,61 31 1 660 3,67 32 1 800 4,00 13 1 640 3,19 44 0 520 2,93 4
Như chúng ta có thể thấy từ đầu ra ở trên, một tên cột là 'rank', điều này có thể tạo ra vấn đề vì 'rank' cũng là tên của phương thức trong khung dữ liệu gấu trúc. Để tránh bất kỳ xung đột nào, tôi đang thay đổi tên của cột xếp hạng thành "uy tín". Vì vậy, hãy thay đổi tên cột tập dữ liệu:
df.columns =["thừa nhận", "gre", "gpa", "uy tín"] print (df.columns)
Đầu ra
Chỉ mục (['thừa nhận', 'gre', 'gpa', 'uy tín'], dtype ='object') Trong []:
Bây giờ mọi thứ có vẻ ổn, bây giờ chúng ta có thể xem xét sâu hơn những gì tập dữ liệu của chúng ta chứa.
# Tóm tắt dữ liệu
Sử dụng hàm pandas mô tả, chúng tôi sẽ có được cái nhìn tóm tắt về mọi thứ.
print (df.describe ())
Đầu ra
thừa nhận gre GPA prestigecount 400.000000 400.000000 400.000000 400.00000mean 0,317500 587,700000 3,389900 2.48500std 0,466087 115,516536 0,380567 0.94446min 0,000000 220,000000 2,260000 1,0000025% 0,000000 520,000000 3,130000 2,0000050% 0,000000 580,000000 3,395000 2,0000075% 1,000000 660,000000 3,670000 3.00000max 1,000000 800,000000 4,000000 4,00000
Chúng tôi có thể nhận được độ lệch chuẩn của từng cột dữ liệu của chúng tôi và bảng tần suất cắt uy tín và liệu ai đó có được nhận hay không.
# hãy xem độ lệch chuẩn của từng cột (df.std ())
Đầu ra
thừa nhận 0,466087gre 115,516536gpa 0,380567prestige 0,944460dtype:float64
Ví dụ
>Đầu ra
uy tín 1 2 3 4admit0 28 97 93 551 33 54 28 12
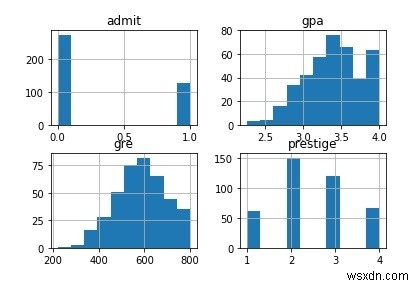
Hãy vẽ tất cả các cột của tập dữ liệu.
# vẽ tất cả các cộtdf.hist () pl.show ()
Đầu ra
Biến giả
Thư viện gấu trúc Python cung cấp tính linh hoạt tuyệt vời trong cách chúng tôi biểu diễn các biến phân loại.
# dummify rankdummy_ranks =pd.get_dummies (df ['uy tín'], prefix ='uy tín') print (dummy_ranks.head ())
Đầu ra
uy tín_1 uy tín_2 uy tín_3 uy tín_40 0 0 1 01 0 0 1 02 1 0 0 03 0 0 0 14 0 0 0 1
Ví dụ
# tạo khung dữ liệu rõ ràng cho regressioncols_to_keep =['inherit', 'gre', 'gpa'] data =df [cols_to_keep] .join (dummy_ranks.ix [:, 'uy tín_2':])
Đầu ra
thừa nhận gre gpa uy tín_2 uy tín_3 uy tín_40 0 380 3,61 0 1 01 1 660 3,67 0 1 02 1 800 4,00 0 0 03 1 640 3,19 0 0 14 0 520 2,93 0 0 1Trong []:
Thực hiện hồi quy
Bây giờ chúng ta sẽ thực hiện hồi quy logistic, điều này khá đơn giản. Chúng tôi chỉ cần chỉ định cột chứa biến mà chúng tôi đang cố gắng dự đoán, sau đó là các cột mà mô hình sẽ sử dụng để đưa ra dự đoán.
Bây giờ chúng tôi dự đoán cột thừa nhận dựa trên các biến giả grey, gpa và uy tín uy tín_2, uy tín_3 &uy tín_4.
# phù hợp với modelresult =logit.fit ()Đầu ra
Quá trình tối ưu hóa đã kết thúc thành công. Giá trị hàm hiện tại:0,573147 Hoạt động 6
Diễn giải kết quả
Hãy tạo kết quả tóm tắt bằng cách sử dụng mô hình thống kê.
print (result.summary2 ())
Đầu ra
Kết quả:Đăng nhập ===============================================================Mô hình:Số lần đăng nhập Số lần lặp lại:6.0000 Biến phụ thuộc:thừa nhận Pseudo R-bình phương:0.083 Ngày:2019-03-03 14:16 AIC:470.5175 Không. Quan sát:400 BIC:494.4663Df Mô hình:5 Khả năng ghi nhật ký:-229,26Df Dư:394 LL-Null:-249.99 Hội tụ:1.0000 Tỷ lệ:1.0000 ------------------ ---------------------------------------------- Rạn san hô. Std.Err. z P> | z | [0,025 0,975] ---------------------------------------------- ------------------ gre 0,0023 0,0011 2,0699 0,0385 0,0001 0,0044gpa 0,8040 0,3318 2,4231 0,0154 0,1537 1,4544prestige_2 -0,6754 0,3165 -2.1342 0,0328 -1,2958 -0,0551prestige_3 -1,3402 0,3453 -3,8812 0,0001 -2.0170 -0.6634prestige_4 -1.5515 0.4178 -3.7131 0.0002 -2.3704 -0.7325 Intercept -3.9900 1.1400 -3.5001 0.0005 -6.2242-11.7557 ===============================================================
Đối tượng kết quả ở trên cũng cho phép chúng tôi cô lập và kiểm tra các phần của đầu ra mô hình.
# xem khoảng tin cậy của mỗi hệ số (result.conf_int ())
Đầu ra
0 1gre 0,000120 0,004409gpa 0,153684 1,454391prestige_2 -1.295751 -0.055135prestige_3 -2.016992 -0,663416prestige_4 -2.370399-0,732529intercept -6.224242-11.755716
Từ kết quả trên, chúng ta có thể thấy có mối quan hệ nghịch đảo b / w xác suất được nhận vào và uy tín của trường đại học của ứng viên.
Vì vậy, xác suất ứng viên được chấp nhận vào chương trình sau đại học sẽ cao hơn đối với những sinh viên đã theo học tại một trường đại học được xếp hạng cao nhất (uy tín_1 =True) so với trường có xếp hạng thấp hơn (uy tín_3 hoặc uy tín_4).
