Chương trình Python cho các thuật toán Euclid mở rộng

Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu hỏi được đưa ra bên dưới.

Tuyên bố sự cố - Cho hai số ta cần tính gcd của hai số đó và hiển thị chúng.

GCD Ước chung lớn nhất của hai số là số lớn nhất có thể chia cả hai số đó. Ở đây chúng tôi làm theo phương pháp euclide để tính toán gcd, tức là chia nhiều lần các số và dừng lại khi phần dư trở thành 0. Ở đây chúng tôi mở rộng thuật toán dựa trên các giá trị trước đó thu được trong đệ quy.

Bây giờ chúng ta hãy quan sát giải pháp trong việc triển khai bên dưới -

Ví dụ

# extended Euclidean Algorithm
def gcdExtended(a, b, x, y):
   # Base Case
   if a == 0 :
      x = 0
      y = 1
      return b
   x1 = 1
   y1 = 1 # storing the result
   gcd = gcdExtended(b%a, a, x1, y1)
   # Update x and y with previous calculated values
   x = y1 - (b/a) * x1
   y = x1
   return gcd
x = 1
y = 1
a = 11
b = 15
g = gcdExtended(a, b, x, y)
print("gcd of ", a , "&" , b, " is = ", g)

Đầu ra

gcd of 11 & 15 is = 1

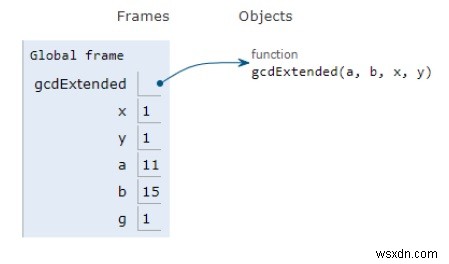
Tất cả các biến được khai báo trong phạm vi cục bộ và các tham chiếu của chúng được hiển thị trong hình trên.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về cách tạo Chương trình Python cho các thuật toán Euclid mở rộng