Giả sử một cuộc đua sẽ được tổ chức. Nơi những viên đá khác nhau được đặt trên một con đường. Một thùng có mặt tại điểm xuất phát của cuộc đua, thùng này cách viên đá đầu tiên 6 đơn vị. Các viên đá còn lại cách nhau 4 đơn vị và lần lượt nằm thẳng hàng. Bây giờ, những người tham gia bắt đầu từ cái xô, sau đó thu thập viên đá gần nhất, quay lại và đặt viên đá đó vào thùng, sau đó chạy lại để thu thập viên đá gần nhất tiếp theo, chạy trở lại và cho vào thùng. Quá trình này sẽ được tiếp tục cho đến khi tất cả đá đã được cho vào thùng. Nếu có n viên đá, thì chúng ta phải tìm tổng khoảng cách cần phải che cho những người tham gia.
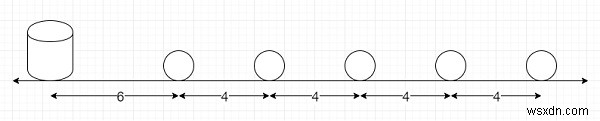
Vì vậy, nếu đầu vào là n =5, thì đầu ra sẽ là 140 là 2 * 6 + 2 (6 + 4) + 2 (6 + 4 + 4) + 2 (6 + 4 + 4 + 4) + 2 (6 + 4 + 4 + 4 + 4) =140
Để giải quyết điều này, chúng ta phải giải phương trình này -
-
Đối với đá 1, chúng ta phải phủ (6 + 6) =2 * 6 khoảng cách
-
Đối với đá 2, chúng ta phải phủ ((6 + 4) + (6 + 4)) =2 * (6 + 4) khoảng cách
-
Đối với đá 3, chúng ta phải phủ ((6 + 4 + 4) + (6 + 4 + 4)) =2 * (6 + 4 + 4) khoảng cách
-
Đối với đá n, chúng ta phải bao gồm ((6 + 4 * (n-1)) + (6 + 4 * (n-1))) =2 * (6 + 4 * (n-1)) khoảng cách
Đối với tất cả các loại đá, chúng tôi phải phủ -
-
D =2 * 6 + 2 * (6 + 4) + 2 * (6 + 4 + 4) +… + 2 * (6 + 4 * (n-1))
-
D =2 * [6 + (6 + 4) + (6 + 2 * 4) +… + (6+ (n-1) * 4)]
-
D =2 * [6n + 4 (1 + 2 +… + (n-1))]
-
D =2 * [6n + 4 (n * (n-1) / 2)]
-
D =2 * [6n + 2 (n * (n-1))]
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def find_distance(n): return 2*(6*n + 2*((n-1)*n)) n = 5 print(find_distance(n))
Đầu vào
5
Đầu ra
140
