Tìm số cặp đỉnh phân biệt có khoảng cách chính xác là k trong một cây bằng Python

Giả sử chúng ta có một số nguyên k và cũng có một cây với n nút, chúng ta phải đếm số cặp đỉnh phân biệt có khoảng cách chính xác là k.

Vì vậy, nếu đầu vào là k =2

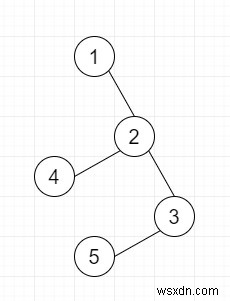
thì đầu ra sẽ là 4

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• N:=5005

• graph:=danh sách gần kề có kích thước N

• vertex_count:=ma trận 2d có kích thước 505 x 5005

• res:=0

• Định nghĩa một hàm insert_edge (). Điều này sẽ mất x, y

  • chèn y vào cuối biểu đồ [x]

  • chèn x vào cuối biểu đồ [y]

• Định nghĩa một hàm dfs (). Điều này sẽ lấy v, cha mẹ

• vertex_count [v, 0]:=1

• đối với mỗi i trong biểu đồ [v], thực hiện

  • nếu tôi không giống cha mẹ, thì

    • dfs (i, v)

    • đối với j trong phạm vi 1 đến k + 1, thực hiện

      • res:=res + vertex_count [i, j - 1] * vertex_count [v, k - j]

    • đối với j trong phạm vi 1 đến k + 1, thực hiện

      • vertex_count [v, j]:=vertex_count [v, j] + vertex_count [i, j - 1]

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

N = 5005
graph = [[] for i in range(N)]
vertex_count = [[0 for i in range(505)] for i in range(N)]
res = 0
def insert_edge(x, y):
   graph[x].append(y)
   graph[y].append(x)
def dfs(v, parent):
   global res
   vertex_count[v][0] = 1
   for i in graph[v]:
      if (i != parent):
         dfs(i, v)
         for j in range(1, k + 1):
            res += vertex_count[i][j - 1] * vertex_count[v][k - j]
         for j in range(1, k + 1):
            vertex_count[v][j] += vertex_count[i][j - 1]
k = 2
insert_edge(1, 2)
insert_edge(2, 3)
insert_edge(3, 4)
insert_edge(2, 5)
dfs(1, 0)
print(res)

Đầu vào

k = 2
insert_edge(1, 2)
insert_edge(2, 3)
insert_edge(3, 4)
insert_edge(2, 5)

Đầu ra

4