Tìm xem một biểu đồ vô hướng có chứa một tập hợp độc lập có kích thước đã cho bằng Python hay không

Giả sử chúng ta có một đồ thị vô hướng đã cho; chúng ta phải kiểm tra xem nó có chứa một tập hợp kích thước l độc lập hay không. Nếu có bất kỳ tập hợp kích thước l độc lập nào thì trả về Có nếu không thì không.

Chúng ta phải lưu ý rằng một tập hợp độc lập trong đồ thị được định nghĩa là một tập hợp các đỉnh không được kết nối trực tiếp với nhau.

Vì vậy, nếu đầu vào là L =4,

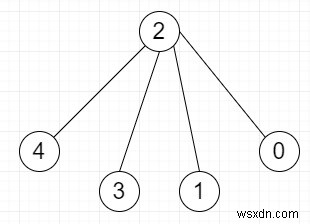
thì đầu ra sẽ là có

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Định nghĩa một hàm is_valid (). Điều này sẽ có biểu đồ, arr

• đối với tôi trong phạm vi từ 0 đến kích thước của arr, thực hiện

  • đối với j trong phạm vi i + 1 đến kích thước của arr, thực hiện

    • nếu đồ thị [arr [i], arr [j]] giống 1 thì

      • trả về Sai

• trả về True

• Định nghĩa một hàm giải quyết (). Điều này sẽ lấy đồ thị, arr, k, index, sol

• nếu k giống 0 thì

  • nếu is_valid (graph, arr) giống True thì

    • sol [0]:=Đúng

    • trở lại

  • nếu không,

    • nếu chỉ mục> =k, thì

      • return (giải quyết (đồ thị, arr [từ chỉ số 0 đến cuối] nối danh sách với [chỉ mục], k-1, chỉ số-1, sol) hoặc giải quyết (đồ thị, arr [từ chỉ số 0 đến cuối], k, chỉ mục- 1, sol))

    • nếu không,

      • trả về giải quyết (đồ thị, arr [từ chỉ mục 0 đến cuối] nối danh sách với [chỉ mục], k-1, chỉ mục-1, sol)

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

def is_valid(graph, arr):
   for i in range(len(arr)):
      for j in range(i + 1, len(arr)):
         if graph[arr[i]][arr[j]] == 1:
            return False
   return True
def solve(graph, arr, k, index, sol):
   if k == 0:
      if is_valid(graph, arr) == True:
         sol[0] = True
         return
      else:
         if index >= k:
            return (solve(graph, arr[:] + [index], k-1, index-1, sol) or solve(graph, arr[:], k, index-1, sol))
         else:
            return solve(graph, arr[:] + [index], k-1, index-1, sol)

graph = [
   [1, 1, 0, 0, 0],
   [1, 1, 1, 1, 1],
   [0, 1, 1, 0, 0],
   [0, 1, 0, 1, 0],
   [0, 1, 0, 0, 1]]
k = 4
arr = []
sol = [False]
solve(graph, arr[:], k, len(graph)-1, sol)
if sol[0]:
   print("Yes")
else:
   print("No")

Đầu vào

[[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1]],
4

Đầu ra

Yes