Giả sử chúng ta có một Cây nhị phân; chúng ta phải tìm kích thước của cây con hoàn chỉnh tối đa trong Cây nhị phân này. Như chúng ta biết một cây nhị phân hoàn chỉnh là Cây nhị phân nếu tất cả các cấp đều được lấp đầy hoàn toàn mà không có cấp cuối cùng và cấp cuối cùng có tất cả các khóa còn lại hết mức có thể.
Vì vậy, nếu đầu vào giống như
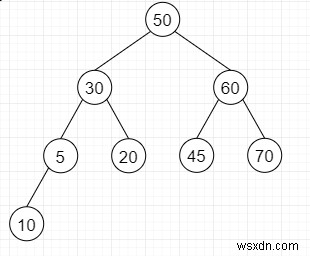
thì đầu ra sẽ là 4 như kích thước và truyền tải nhỏ hơn sẽ là 10, 45, 60, 70,
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định kiểu trả về với một số tham số như isComplete, isPerfect, ban đầu những tham số này là false, sau đó là kích thước và rootTree, kích thước ban đầu là 0 và rootTree là null.
- ret_type:=returnType
- nếu gốc là null, thì
- ret_type.isPerfect:=True
- ret_type.isComplete:=True
- ret_type.size:=0
- ret_type.rootTree:=Không có
- return ret_type
- left_tree:=checkCompleteness (root.left)
- right_tree:=checkCompleteness (root.right)
- if (left_tree.isPerfect là True và right_tree.isComplete là True và chiều cao của cây trái và phải là như nhau, thì
- ret_type.isComplete:=True
- ret_type.isPerfect:=right_tree.isPerfect
- ret_type.size:=left_tree.size + right_tree.size + 1
- ret_type.rootTree:=root
- return ret_type
- if (left_tree.isComplete là True và right_tree.isPerfect là True và chiều cao của cây trái và phải là như nhau, thì
- ret_type.isComplete:=True
- ret_type.isPerfect:=Sai
- ret_type.size:=left_tree.size + right_tree.size + 1
- ret_type.rootTree:=root
- return ret_type
- ret_type.isPerfect:=Sai
- ret_type.isComplete:=Sai
- ret_type.size:=tối đa left_tree.size, right_tree.size
- nếu left_tree.size> right_tree.size, thì
- ret_type.rootTree:=left_tree.rootTree
- nếu không,
- ret_type.rootTree:=right_tree.rootTree
- return ret_type
Python
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
import math
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
class returnType :
def __init__(self):
self.isPerfect = None
self.isComplete = None
self.size = 0
self.rootTree = None
def getHeight(size):
return int(math.ceil(math.log(size + 1)/math.log(2)))
def checkCompleteness(root) :
ret_type = returnType()
if (root == None):
ret_type.isPerfect = True
ret_type.isComplete = True
ret_type.size = 0
ret_type.rootTree = None
return ret_type
left_tree = checkCompleteness(root.left)
right_tree = checkCompleteness(root.right)
if (left_tree.isPerfect == True and right_tree.isComplete == True and getHeight(left_tree.size) == getHeight(right_tree.size)) :
ret_type.isComplete = True
ret_type.isPerfect = right_tree.isPerfect
ret_type.size = left_tree.size + right_tree.size + 1
ret_type.rootTree = root
return ret_type
if (left_tree.isComplete == True and right_tree.isPerfect == True and getHeight(left_tree.size) == getHeight(right_tree.size) + 1):
ret_type.isComplete = True
ret_type.isPerfect = False
ret_type.size = left_tree.size + right_tree.size + 1
ret_type.rootTree = root
return ret_type
ret_type.isPerfect = False
ret_type.isComplete = False
ret_type.size =max(left_tree.size, right_tree.size)
if(left_tree.size > right_tree.size ):
ret_type.rootTree = left_tree.rootTree
else:
ret_type.rootTree = right_tree.rootTree
return ret_type
def print_tree(root):
if root is not None:
print_tree(root.left)
print(root.data, end = ', ')
print_tree(root.right)
root = TreeNode(50)
root.left = TreeNode(30)
root.right = TreeNode(60)
root.left.left = TreeNode(5)
root.left.right = TreeNode(20)
root.right.left = TreeNode(45)
root.right.right = TreeNode(70)
root.right.left.left = TreeNode(10)
ans = checkCompleteness(root)
print( "Size:" , ans.size )
print("Inorder Traversal: ", end = '')
print_tree(ans.rootTree) Đầu vào
root = TreeNode(50) root.left = TreeNode(30) root.right = TreeNode(60) root.left.left = TreeNode(5) root.left.right = TreeNode(20) root.right.left = TreeNode(45) root.right.right = TreeNode(70) root.right.left.left = TreeNode(10)
Đầu ra:
Size: 4 Inorder Traversal: 10, 45, 60, 70,
