Chương trình tìm tổng lớn nhất của đường dẫn giữa hai nút trong cây nhị phân bằng Python

Giả sử chúng ta có một cây nhị phân; chúng ta phải tìm tổng lớn nhất của bất kỳ đường dẫn nào giữa hai nút bất kỳ.

Vì vậy, nếu đầu vào giống như

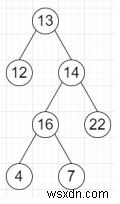
thì đầu ra sẽ là 62 vì các nút là [12,13,14,16,7].

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Định nghĩa một hàm utils (). Điều này sẽ bắt nguồn từ gốc

• nếu root null thì

  • trả về 0

• l:=utils (bên trái của thư mục gốc)

• r:=utils (bên phải của thư mục gốc)

• max_single:=tối đa (tối đa của l và r) + giá trị của gốc) và giá trị của gốc

• max_top:=tối đa của max_single và l + r + giá trị của gốc

• res:=tối đa res và max_top

• trả về max_single

• Từ phương thức chính, thực hiện như sau -

• nếu root là null thì

  • trả về 0

• res:=infinity

• utils (gốc)

• trả lại res

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

class TreeNode:
   def __init__(self, value):
      self.val = value
      self.left = None
      self.right = None
class Solution:
   def solve(self, root):
      if root is None:
         return 0
      self.res = float("-inf")
      self.utils(root)
      return self.res
   def utils(self, root):
      if root is None:
         return 0
      l = self.utils(root.left)
      r = self.utils(root.right)
      max_single = max(max(l, r) + root.val, root.val)
      max_top = max(max_single, l + r + root.val)
      self.res = max(self.res, max_top)
      return max_single
ob = Solution()
root = TreeNode(13)
root.left = TreeNode(12)
root.right = TreeNode(14)
root.right.left = TreeNode(16)
root.right.right = TreeNode(22)
root.right.left.left = TreeNode(4)
root.right.left.right = TreeNode(7)
print(ob.solve(root))

Đầu vào

root = TreeNode(13)
root.left = TreeNode(12)
root.right = TreeNode(14)
root.right.left = TreeNode(16)
root.right.right = TreeNode(22)
root.right.left.left = TreeNode(4)
root.right.left.right = TreeNode(7)

Đầu ra

62