Các vectơ Eigen và các giá trị Eigen được sử dụng trong nhiều trường hợp. Từ ‘Eigen’ trong tiếng Đức có nghĩa là ‘riêng’ hoặc ‘điển hình’. Vectơ Eigen còn được gọi là 'vectơ đặc trưng'. Giả sử chúng ta cần thực hiện một số chuyển đổi trên tập dữ liệu nhưng điều kiện đã cho là hướng của dữ liệu trong tập dữ liệu không được thay đổi. Đây là lúc các vectơ Eigen và các giá trị Eigen có thể được sử dụng.
Cho một ma trận vuông (ma trận trong đó số hàng bằng số cột), một giá trị Eigen và một vectơ Eigen đáp ứng phương trình dưới đây.
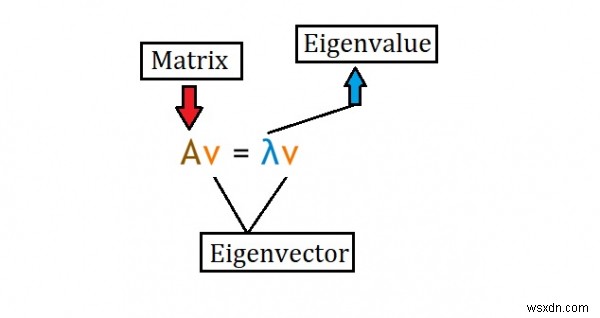
Các vectơ Eigen được tính sau khi tìm thấy các giá trị Eigen.
Lưu ý - Giá trị Eigen cũng hoạt động tốt với các thứ nguyên 3 hoặc lớn hơn.
Thay vì điều chỉnh thủ công các phép tính toán học này, SciPy cung cấp một hàm trong thư viện có tên là ‘eig’ giúp tính toán Eigenvalue và Eigenvector.
Cú pháp của hàm 'eig'
scipy.linalg.eig(matrix)
Hãy để chúng tôi xem cách sử dụng hàm ‘eig’ -
Ví dụ
from scipy import linalg
import numpy as np
my_arr = np.array([[5,7],[11,3]])
eg_val, eg_vect = linalg.eig(my_arr)
print("The Eigenvalues are :")
print(eg_val)
print("The Eigenvectors are :")
print(eg_vect) Đầu ra
The Eigenvalues are : [12.83176087+0.j -4.83176087+0.j] The Eigenvectors are : [[ 0.66640536 -0.57999285] [ 0.74558963 0.81462157]]
Giải thích
- Các thư viện bắt buộc đã được nhập.
- Ma trận được xác định với các giá trị nhất định trong đó, sử dụng thư viện Numpy.
- Ma trận được chuyển dưới dạng tham số cho hàm 'eig' để tính toán các giá trị riêng và các giá trị riêng của ma trận.
- Dữ liệu được tính toán này được lưu trữ trong hai biến khác nhau.
- Kết quả đầu ra này được hiển thị trên bảng điều khiển.
