Chương trình tìm bao nhiêu dòng cắt nhau trong Python

Giả sử chúng ta được đưa ra một danh sách chứa các giá trị theo cặp (m, c). Các giá trị này đại diện cho một đường, trong đó y =mx + c. Chúng tôi cũng được cung cấp hai giá trị, l và r. Chúng ta phải tìm ra số lượng các đường thẳng cắt nhau trong khoảng từ x =l đến x =h.

Vì vậy, nếu đầu vào là input_list =[[4, 6], [- 6, 10], [8, 12]], l =0, h =2, thì đầu ra sẽ là 2.

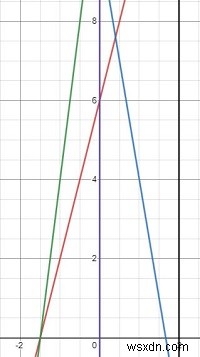
Nếu chúng ta nhìn vào bức ảnh đã cho, các đường thẳng 4x + 6 =0 và -6x + 10 cắt nhau trong phạm vi đã cho. Vì vậy, có hai đường thẳng cắt nhau, do đó, kết quả là 2.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• seg:=danh sách chứa các cặp [(m * l + c, m * h + c, i) cho chỉ mục i và các giá trị (m, c) trong input_list]
• sắp xếp danh sách seg
• ans:=một danh sách mới có kích thước của input_list chứa các số 0
• c:=một bản đồ mới từ seg
• cho mỗi (x, y, i) trong seg, thực hiện
  • nếu c [x]> 1, thì
    • ans [i]:=1
• max_c:=- (10 ^ 10)
• prv:=- (10 ^ 10)
• cho mỗi (x, y, i) trong seg, thực hiện
  • nếu x giống với prv, thì
    • ans [i]:=1
  • nếu y <=max_c, thì
    • ans [i]:=1
  • max_c:=tối đa của (max_c, y)
    • prv:=x
• min_c =10 ^ 10
• prv =10 ^ 10
• đối với mỗi (x, y, i) trong seg được đảo ngược, thực hiện
  • nếu x giống với prv, thì
    • ans [i]:=1
  • nếu y> =min_c, thì
    • ans [i]:=1
  • min_c:=tối thiểu là (min_c, y)
  • prv:=x
• trả về tổng các phần tử của danh sách (ans)

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

from collections import Counter

def solve(input_list, l, h):
   seg = [(m * l + c, m * h + c, i) for i, (m, c) in
enumerate(input_list)]
   seg.sort()
   ans = [0 for _ in input_list]
   c = Counter(seg)
   for (x, y, i) in seg:
      if c[x] > 1:
         ans[i] = 1
   max_c = -(10 ** 10)
   prv = -(10 ** 10)
   for (x, y, i) in seg:
      if x == prv:
         ans[i] = 1
      if y <= max_c:
         ans[i] = 1
      max_c = max(max_c, y)
      prv = x
   min_c = 10 ** 10
   prv = 10 ** 10
   for (x, y, i) in seg[::-1]:
      if x == prv:
         ans[i] = 1
      if y >= min_c:
         ans[i] = 1
      min_c = min(min_c, y)
      prv = x
   return sum(ans)

print(solve([[4, 6],[-6, 10],[8, 12]], 0, 2))

Đầu vào

[[4, 6],[-6, 10],[8, 12]], 0, 2

Đầu ra

2