Giả sử, có một số hình khối có kích thước a, b và c, và sử dụng chúng một hộp mới có kích thước axbxc được tạo ra. a, b, và c là đồng nguyên tố từng cặp; gcd (a, b) =gcd (b, c) =gcd (c, d) =1. Ta phải cắt cái hộp thành hai mảnh có một lát như trong hình. Ta phải tìm xem cái hộp được cắt theo cách này thì có bao nhiêu hình lập phương được cắt thành hai mảnh. Chúng tôi được cung cấp một mảng chứa ba chiều có thể có và chúng tôi phải tìm ra câu trả lời của mình từ đó.
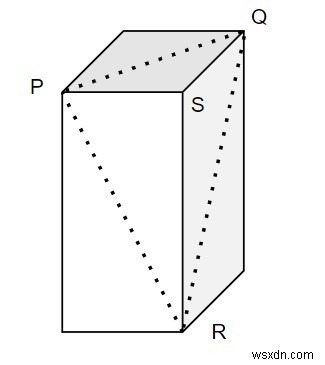
Hình cắt được thực hiện theo cách đó là mặt phẳng đi qua các đỉnh P, Q và R.
Vì vậy, nếu đầu vào là n =3, input_array =[[1, 2, 3], [4, 2, 5], [6, 8, 2]], thì đầu ra sẽ là [5, 18, 37 ]
Có 3 trường hợp khác nhau được đưa ra và chúng ta phải tìm ra số hình lập phương bị cắt. Nếu khối lập phương được cắt theo cách như trong hình; 5, 16 và 37 hình khối được cắt tương ứng.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau &miuns;
- output:=một danh sách mới
- đối với tôi trong phạm vi từ 0 đến n, thực hiện
- a:=input_array [i, 0]
- b:=input_array [i, 1]
- c:=input_array [i, 2]
- val:=giá trị sàn của (a * b + a * c + b * c - 1) / 2 mod 1000000007
- chèn val vào cuối đầu ra
- trả về kết quả đầu ra
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
from math import ceil def solve(n, input_array): output = [] for i in range(n): a, b, c = input_array[i][0], input_array[i][1], input_array[i][2] val = ((a * b + a * c + b * c - 1) // 2 % 1000000007) output.append(val) return output print(solve(3, [[1, 2, 3], [4, 2, 5], [6, 8, 2]]))
Đầu vào
3, [[1, 2, 3], [4, 2, 5], [6, 8, 2]]
Đầu ra
[5, 18, 37]
