Trong phương pháp duyệt này, cây con bên trái được truy cập đầu tiên, sau đó là cây gốc và sau đó là cây con bên phải. Chúng ta nên luôn nhớ rằng mỗi nút có thể đại diện cho chính một cây con.
Nếu cây nhị phân được duyệt theo thứ tự , đầu ra sẽ tạo ra các giá trị khóa được sắp xếp theo thứ tự tăng dần.
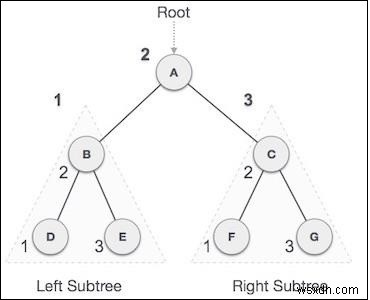
Chúng tôi bắt đầu từ A, và theo dõi duyệt theo thứ tự, chúng ta chuyển sang cây con bên trái của nó B. B cũng được duyệt theo thứ tự. Quá trình tiếp tục cho đến khi tất cả các nút được truy cập. Đầu ra của quá trình di chuyển ngang qua cây này sẽ là -
D → B → E → A → F → C → G
Đây là thuật toán chúng tôi sẽ triển khai -
- Đi qua đệ quy bên trái một cách đệ quy
- In dữ liệu của nút
- Đệ quy đi qua cây con bên phải
Hãy để chúng tôi xem cách chúng tôi sẽ triển khai nó trong lớp học của chúng tôi. Vì chúng tôi không muốn người dùng tự chuyển quyền root nên chúng tôi sẽ tạo một hàm trợ giúp bên ngoài lớp.
inOrder() {
inOrderHelper(this.root);
} Chức năng người trợ giúp -
Ví dụ
function inOrderHelper(root) {
if (root !== null) {
inOrderHelper(root.left);
console.log(root.data);
inOrderHelper(root.right);
}
} Bạn có thể kiểm tra điều này bằng cách sử dụng -
Ví dụ
let BST = new BinarySearchTree(); BST.insertRec(10); BST.insertRec(15); BST.insertRec(5); BST.insertRec(50); BST.insertRec(3); BST.insertRec(7); BST.insertRec(12); BST.inOrder();
Đầu ra
Điều này sẽ cung cấp đầu ra -
3 5 7 10 12 15 50
Lưu ý rằng các phần tử được in theo thứ tự được sắp xếp. Điều này là do vì chúng ta khám phá một cách đệ quy cây con bên trái một cách đệ quy trước, nên chúng ta nhận được các giá trị nhỏ nhất trước tiên. Điều này tiếp tục diễn ra cho đến cuối cùng và chúng tôi nhận được tất cả các yếu tố theo một thứ tự được sắp xếp.
