DFS thăm các đỉnh con trước khi thăm các đỉnh anh em; nghĩa là, nó đi qua độ sâu của bất kỳ con đường cụ thể nào trước khi khám phá bề rộng của nó. Một ngăn xếp (thường là ngăn xếp cuộc gọi của chương trình thông qua đệ quy) thường được sử dụng khi triển khai thuật toán.
Sau đây là cách DFS hoạt động -
- Ghé thăm đỉnh không được chờ đợi liền kề. Đánh dấu nó là đã ghé thăm. Hiển thị nó. Đẩy nó vào một ngăn xếp.
- Nếu không tìm thấy đỉnh liền kề, hãy bật lên một đỉnh từ ngăn xếp. (Nó sẽ bật lên tất cả các đỉnh từ ngăn xếp, những đỉnh không có các đỉnh liền kề.)
- Lặp lại Quy tắc 1 và Quy tắc 2 cho đến khi ngăn xếp trống.
Chúng ta hãy xem minh họa về cách hoạt động của DFS.
| Bước | Truyền tải | Mô tả |
|---|---|---|
| 1 |  | Khởi tạo ngăn xếp. |
| 2 | 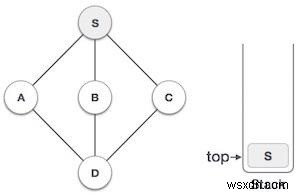 | Đánh dấu S như đã thăm và đặt nó vào ngăn xếp. Khám phá bất kỳ nút liền kề chưa được kiểm tra nào từ S . Chúng tôi có ba nút và chúng tôi có thể chọn bất kỳ nút nào trong số chúng. Đối với ví dụ này, chúng ta sẽ lấy nút theo thứ tự bảng chữ cái. |
| 3 | 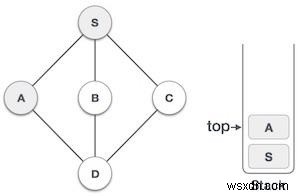 | Đánh dấu A như đã thăm và đặt nó vào ngăn xếp. Khám phá bất kỳ nút liền kề chưa được kiểm tra nào từ A . Cả S và D liền kề với A nhưng chúng tôi chỉ quan tâm đến các nút không được truy cập. |
| 4 | 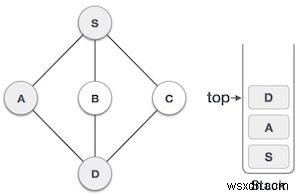 | Truy cập D và đánh dấu nó là đã thăm và đặt vào ngăn xếp. Ở đây, chúng tôi có B và C các nút tiếp giáp với D và cả hai đều không được mời. Tuy nhiên, chúng ta sẽ lại chọn theo thứ tự bảng chữ cái. |
| 5 | 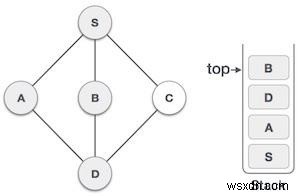 | Chúng tôi chọn B, đánh dấu nó là đã thăm và đặt vào ngăn xếp. Đây B không có bất kỳ nút liền kề không được truy cập nào. Vì vậy, chúng tôi bật B từ ngăn xếp. |
| 6 | 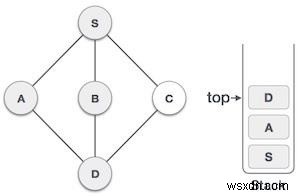 | Chúng tôi kiểm tra đỉnh ngăn xếp xem có quay trở lại nút trước đó không và kiểm tra xem nó có bất kỳ nút nào chưa được truy cập hay không. Tại đây, chúng tôi tìm thấy Đ ở trên cùng của ngăn xếp. |
| 7 | 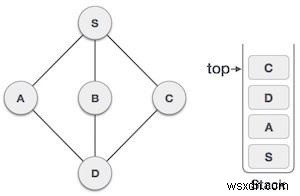 | Chỉ nút liền kề không được truy cập là từ D là C Hiện nay. Vì vậy, chúng tôi truy cập C, đánh dấu nó là đã thăm và đặt nó vào ngăn xếp. |
Như C không có bất kỳ nút liền kề nào chưa được duyệt, vì vậy chúng tôi tiếp tục bật ngăn xếp cho đến khi chúng tôi tìm thấy một nút có nút liền kề không được truy cập. Trong trường hợp này, không có gì và chúng tôi tiếp tục xuất hiện cho đến khi ngăn xếp trống. Hãy để chúng tôi xem cách chúng tôi có thể triển khai điều này trong JavaScript.
Ví dụ
DFS(node) {
// Create a Stack and add our initial node in it
let s = new Stack(this.nodes.length);
let explored = new Set();
s.push(node);
// Mark the first node as explored
explored.add(node);
// We'll continue till our Stack gets empty
while (!s.isEmpty()) {
let t = s.pop();
// Log every element that comes out of the Stack
console.log(t);
// 1. In the edges object, we search for nodes this node is directly connected to.
// 2. We filter out the nodes that have already been explored.
// 3. Then we mark each unexplored node as explored and push it to the Stack.
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
s.push(n);
});
}
} Chà, điều đó thật dễ dàng. Chúng tôi thực sự chỉ hoán đổi hàng đợi cho ngăn xếp và thì đấy, chúng tôi có DFS. Đó thực sự là sự khác biệt duy nhất giữa 2. DFS cũng có thể được thực hiện bằng cách sử dụng đệ quy. Nhưng điều đó là tốt nhất nên tránh trong trường hợp này vì biểu đồ lớn hơn có nghĩa là chúng ta cần thêm bộ nhớ chỉ để theo dõi ngăn xếp cuộc gọi.
Bạn có thể kiểm tra điều này bằng cách sử dụng -
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.DFS("A"); Đầu ra
Điều này sẽ cung cấp đầu ra.
A D E F B G C
