Liên kết số là một loại câu đố logic liên quan đến việc tìm đường dẫn để kết nối các số trong một lưới.

Một ví dụ đơn giản về câu đố Numberlink Giải pháp cho câu đố Numberlink
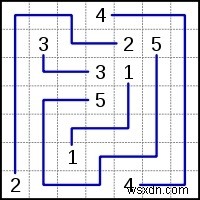
Quy tắc - Người chơi phải ghép tất cả các số phù hợp trên lưới với các đường (hoặc đường dẫn) liên tục. Các dòng không được phân nhánh hoặc cắt chéo nhau và các con số phải nằm ở cuối mỗi dòng (tức là không nằm ở giữa). Một vấn đề được coi là được thiết kế tốt chỉ khi nó có một giải pháp duy nhất và tất cả các ô trong lưới đều được lấp đầy, mặc dù một số nhà thiết kế Numberlink không quy định điều này.
Trò chơi - Xét một mảng hình vuông n × n. Một số ô trống, một số ô liền và một số ô không đặc được đánh dấu bằng các số nguyên 1, 2, 3,… Mỗi số nguyên chiếm đúng hai ô vuông khác nhau trên bảng. Nhiệm vụ của người chơi là kết nối hai lần xuất hiện của mỗi số nguyên trên bàn cờ bằng một con đường đơn giản chỉ sử dụng các chuyển động ngang và dọc. Không được phép có hai con đường khác nhau cắt nhau. Không có con đường nào có thể bao gồm bất kỳ hình vuông đặc nào (các hình vuông đặc bị cấm xuất hiện trên bất kỳ con đường nào). Cuối cùng, tất cả các hình vuông không liền khối phải được lấp đầy bởi các đường dẫn.
Thuật toán - Để chuẩn bị một câu đố ngẫu nhiên hợp lệ với kích thước bảng đã cho là n × n, trước tiên chúng ta tạo các đường dẫn ngẫu nhiên đơn giản không giao nhau trên bảng. Nếu một vài hình vuông cô lập vẫn nằm ngoài tất cả các đường dẫn đã tạo, hãy đánh dấu những hình vuông cô lập này là rắn (bị cấm). Sau đó, chúng tôi cung cấp các điểm cuối của các đường dẫn và danh sách các hình vuông đặc làm câu đố.
Vì vậy, trước tiên chúng tôi tạo ra một giải pháp và sau đó tìm ra câu đố từ giải pháp. Các đường dẫn và các ô vuông đặc phân vùng bảng n × n. Chúng tôi sử dụng cấu trúc dữ liệu union-find để tạo phân vùng này. Cấu trúc dữ liệu xử lý các tập con của tập hợp n ^ 2 ô vuông trên bảng.
Giải thích
-
Xác định vị trí các ô vuông (i, j) và (k, l) ngẫu nhiên trên bảng sao cho:(a) (i, j) và (k, l) là hàng xóm của nhau và (b) không phải (i, j) nor (k, l) thuộc bất kỳ đường dẫn nào được tạo cho đến nay. Nếu không tìm thấy cặp hình vuông nào như vậy trên toàn bộ bảng, hãy trả về FAILURE / * Ở đây, (i, j) và (k, l) là hai hình vuông đầu tiên trên đường mới sẽ được xây dựng. *
-
Tạo sự kết hợp của hai cây tìm kiếm kết hợp chứa (i, j) và (k, l).
-
Lặp lại miễn là có thể mở rộng đường dẫn hiện tại:Đổi tên (i, j) =(k, l). Định vị một bình phương lân cận ngẫu nhiên (k, l) của (i, j) sao cho:(a) (k, l) không thuộc bất kỳ đường dẫn nào được tạo cho đến nay (kể cả đường hiện tại) (b) người hàng xóm duy nhất (k , l) có trên đường dẫn hiện tại được xây dựng một phần là (i, j).
-
Nếu không tìm thấy hàng xóm (k, l) như vậy, đường dẫn không thể được mở rộng thêm, vì vậy hãy ngắt vòng lặp
-
Nếu không, hãy tạo sự kết hợp của hai cây tìm kết hợp mà (i, j) và (k, l) thuộc về.
-
Đặt cờ điểm cuối của hai hình vuông ở đầu và cuối của đường dẫn mới.
-
Trở lại THÀNH CÔNG
Đầu vào
| || || || || || || 4 | | || || || || || 3 || | | || || 2 || 2 || || || 3 | | || || || || X || || 1 | | || || 6 || || || 7 || 7 | | 5 || 4 || || X || || X || 1 | | || 5 || || 6 || || || |
Đầu ra
Giải pháp cho bảng trên
| 4 || 4 || 4 || 4 || 4 || 4 || 4 | | 4 || 1 || 1 || 1 || 1 || 3 || 3 | | 4 || 1 || 2 || 2 || 1 || 1 || 3 | | 4 || 1 || 1 || 1 || X || 1 || 1 | | 4 || 4 || 6 || 1 || 1 || 7 || 7 | | 5 || 4 || 6 || X || 1 || X || 1 | | 5 || 5 || 6 || 6 || 1 || 1 || 1 |
Ví dụ
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*
Input:a node Output:the set pointer of the set the node belongs to
Mô tả - Lấy một nút và trả về con trỏ thiết lập. * /
node *findset(node *n) {
if (n->parent != NULL)
n = n->parent;
return n;
}
void setunion(node *x, node *y) {
x = findset(x);
y = findset(y);
if (x->rank > y->rank)
y->parent = x;
else {
x->parent = y;
if(x->rank == y->rank)
y->rank++;
}
}
int neighbour(int n, node ***arr) {
int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
int k = rand()%(n*n);
while (ct < (n*n)) {
k %= (n*n);
i1 = k/n;
j1 = k%n;
if (arr[i1][j1]->path_number==0) {
int kk = rand()%4;
int cc = 0;
switch (kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 4: if(cc==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 5: if(cc==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 6: if(cc==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 7: if(cc==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
}
}
if(flag==1)
break;
ct++;
k++;
}
if(ct<n*n) {
k2= (i2*n)+j2;
return k*(n*n)+k2;
} else {
return -1;
}
}
int checkneigh(int k1, int k2, int n, node ***arr) {
int i= k2/n;
int j= k2%n;
int ii= k1/n;
int jj= k1%n;
int ct=0;
if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
ct++;
if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
ct++;
if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
ct++;
if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
ct++;
if(ct>1)
return 0;
else
return 1;
}
int valid_next(int k, int n, node ***arr) {
int i1, i2, j1, j2, a, b, kk, stat,ct=0;
int flag=0;
i1= k/n;
j1= k%n;
kk= rand()%4;
switch(kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 4: if(ct==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 5: if(ct==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 6: if(ct==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 7: if(ct==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d\n",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
}
//printf("flag- %d\n",flag);
if(flag==0)
return -1;
if(flag) {
//printf("value sent- %d\n", i2*n + j2);
return (i2*n)+j2;
}
}
int addpath(node ***arr, int n, int ptno) {
int a,b,k1,k2;
int i1,j1,i2,j2;
k2= neighbour( n, arr);
if(k2==-1) //no valid pair found to start with
return 0;
k1= k2/(n*n);
k2= k2%(n*n);
//printf("%d %d\n",k1,k2);
i1= k1/n;
j1= k1%n;
i2= k2/n;
j2= k2%n;
arr[i1][j1]->endpoint= 1;
arr[i2][j2]->path_number= ptno;
arr[i1][j1]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1, n2);
while(1) {
i1= i2;
j1= j2;
k1= (i1*n)+j1;
k2= valid_next(k1,n,arr);
if(k2==-1) {
arr[i1][j1]->endpoint= 1;
break;
}
i2=k2/n;
j2=k2%n;
arr[i2][j2]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1,n2);
}
return 1;
}
void printtable(node ***arr, int n) {
int i,j;
printf("Table to be solved:\n");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->endpoint ==1){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else if(arr[i][j]->path_number==0)
printf("| X |");
else
printf("| |");
}
printf("\n");
}
printf("\n\nThe solution to the above table:\n");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->path_number != 0){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else
printf("| X |");
}
printf("\n");
}
}
int main(void) {
srand((unsigned int) time (NULL));
int i, j;
int ct = 1;
int n = 7;
node*** pointers= (node ***)malloc(n*sizeof(node **));
for (i=0; i<n; i++)
pointers[i] = (node **)malloc(n*sizeof(node *));
initboard(pointers, n);
while(1) {
i = addpath(pointers, n, ct);
if (i==0) {
break;
} else {
ct++;
}
}
printtable(pointers,n);
return 0;
} 