Chương trình tính diện tích và chu vi hình thoi có các đường chéo cho trước Hình thoi trong C ++ là gì?

Hình thoi là gì?

Trong hình học, hình thoi là tứ giác có độ dài bốn cạnh bằng nhau. Hình thoi giống với hình thoi. Nếu các đường chéo của hình thoi gặp nhau ở góc vuông hơn thì nó sẽ trở thành hình vuông.

Các thuộc tính của hình thoi là -

• các cạnh bằng nhau
• Các cạnh đối diện là song song và các góc đối diện bằng nhau làm cho nó trở thành hình bình hành
• đường chéo chia đôi ở góc vuông

Dưới đây là hình của hình thoi

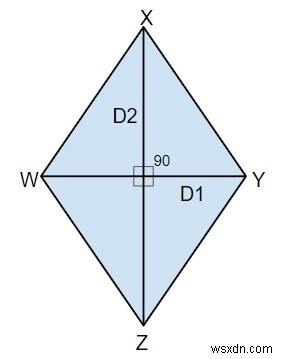
Vấn đề

Với các đường chéo, giả sử d1 và d2, nhiệm vụ là tìm diện tích và chu vi của một hình thoi trong đó diện tích là không gian được chiếm bởi hình dạng và chu vi là không gian mà các ranh giới của nó sẽ bao phủ

Để tính diện tích và chu vi của một hình lập phương, có một công thức -

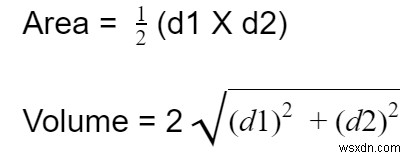
Ví dụ

Input-: d1=6 and d2=12
Output-: The perimeter of rhombus with given diagonals are :26
   The area of rhombus with given diagonals are :36

THUẬT TOÁN

Start
Step 1 -> declare function to calculate perimeter of rhombus
   int perimeter(int d1, int d2)
      Declare variable long long int perimeter
      Set perimeter = 2 * sqrt(pow(d1, 2) + pow(d2, 2))
      Print perimeter
Step 2 -> Declare function to calculate area of rhombus
   int area(int d1, int d2)
      Declare long long int area
      Set area = (d1 * d2) / 2
      Print area
Step 3 -> In main()
   Declare variable int d1 = 6, d2 = 12
   Call perimeter(d1, d2)
   Call area(d1, d2)
Stop

Ví dụ

#include <iostream>
#include <math.h>
using namespace std;
// program to calculate perimeter of rhombus
int perimeter(int d1, int d2){
   long long int perimeter;
   perimeter = 2 * sqrt(pow(d1, 2) + pow(d2, 2));
   cout<< "The perimeter of rhombus with given diagonals are :"<<perimeter;
}
//program to calculate area of rhombus
int area(int d1, int d2){
   long long int area;
   area = (d1 * d2) / 2;
   cout<<"\nThe area of rhombus with given diagonals are :"<< area;
}
int main(){
   int d1 = 6, d2 = 12;
   perimeter(d1, d2);
   area(d1, d2);
   return 0;
}

Đầu ra

The perimeter of rhombus with given diagonals are :26
The area of rhombus with given diagonals are :36