Trong vấn đề này, chúng tôi sẽ tạo một chương trình C để mô phỏng dữ liệu tự động hữu hạn không xác định (NFA).
NFA (Dữ liệu tự động hữu hạn không xác định) máy trạng thái hữu hạn có thể di chuyển đến bất kỳ tổ hợp trạng thái nào cho một ký hiệu đầu vào, tức là không có trạng thái chính xác mà máy sẽ di chuyển.
Định nghĩa chính thức về NDFA -
NFA / NDFA (Dữ liệu tự động hữu hạn không xác định) có thể được biểu diễn bằng 5 bộ (Q, ∑, δ, q0, F) trong đó -
-
Q là một tập hợp hữu hạn các trạng thái.
-
∑ là một tập hợp hữu hạn các ký hiệu được gọi là các bảng chữ cái.
-
δ là hàm chuyển đổi trong đó d:Q × ∑ → 2Q (Ở đây, tập lũy thừa của Q (2Q) đã được lấy vì trong trường hợp NDFA, từ một trạng thái, chuyển đổi có thể xảy ra thành bất kỳ kết hợp nào của Q trạng thái)
-
q0 là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q0 ∈ Q).
-
F là tập hợp các trạng thái / trạng thái cuối cùng của Q (F ⊆ Q).
Trong lập trình, NFA được tạo bằng biểu đồ có hướng. Mỗi đỉnh của biểu đồ biểu thị các trạng thái của NDA. Các cạnh của biểu đồ có thể có một trong hai giá trị 0 hoặc 1. Cạnh được gắn nhãn là 0 đại diện cho quá trình chuyển đổi không chấp nhận trong khi Cạnh được gắn nhãn là 1 đại diện cho quá trình chuyển đổi chấp nhận.
Có một điểm vào biểu đồ nói chung là đỉnh 1 mà từ đó nó nhận chuỗi đầu vào là một mảng nhị phân có độ dài hữu hạn.
Hãy xem một biểu mẫu đồ họa NFA và sau đó giải một ngữ pháp bằng cách sử dụng nó.
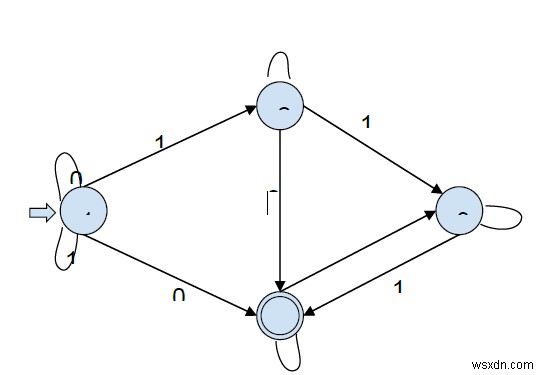
Trạng thái bắt đầu -> 1
Trạng thái cuối cùng (trạng thái chấp nhận) -> 4
Hãy kiểm tra xem chuỗi 01001 có được chấp nhận hay không.
Bắt đầu trạng thái 1, đầu vào 0, với 0, chúng ta có thể chuyển đến trạng thái 4 hoặc vòng lặp tự đến trạng thái 1.
Chúng tôi sẽ xem xét cả hai trường hợp -
{1->1} 1001
{1->4} 1001 Trạng thái 1/4, đầu vào 1 -
Từ trạng thái 1, chúng ta có thể đi đến 2 hoặc tự lặp, Từ trạng thái 4, chúng ta không thể đi xa hơn nên chúng ta sẽ loại bỏ trường hợp này.
Chúng tôi sẽ xem xét các trường hợp từ một -
{1->1->1} 001
{1->1->2} 001 Trạng thái 1/2, đầu vào 0 -
From state 1, we can go to 4 or self-loop, From state 2, we can go to 4 or self-loop
Chúng tôi sẽ xem xét tất cả các trường hợp -
{1->1->1->1} 01
{1->1->1->4} 01
{1->1->2->1} 01
{1->1->2->4} 01 Trạng thái 1/2/4, đầu vào 0 -
From state 1, we can go to 4 or self-loop, From state 2, we can go to 4 or self-loop, From state 4, we can go to 3 or self-loop.
Chúng tôi sẽ xem xét tất cả các trường hợp -
{1->1->1->1->1} 1
{1->1->1->1->4} 1
{1->1->1->4->3} 1
{1->1->1->4->4} 1
{1->1->2->1->1} 1
{1->1->2->1->4} 1
{1->1->2->4->3} 1
{1->1->2->4->4} 1 Trạng thái 1/2/3/4, đầu vào 1 -
From state 1, we can go to 2 or self-loop, From state 2, we can go to 3, From state 3, we can go to 4, From state 4, we cannot go further.
Chúng tôi sẽ xem xét tất cả các trường hợp -
{1->1->1->1->1->1/2} does not reach final stage
{1->1->1->1->4} 1 cannot accept input
{1->1->1->4->3 ->4} accepts the input
{1->1->1->4->4} cannot accept input
{1->1->2->1->1 -> 1/2} does not reach final stage
{1->1->2->1->4} cannot accept input
{1->1->2->4->3->4} accepts the input
{1->1->2->4->4} cannot accept input Do đó, có nhiều cách để đạt đến trạng thái cuối cùng với chuỗi đầu vào đã cho.
Bây giờ, hãy chuyển sang chương trình C để mô phỏng Dữ liệu tự động hữu hạn không xác định (NFA) -
Đầu vào của chương trình sẽ là một danh sách liền kề của NFA -
Số cạnh (n)
Kết nối cạnh (n dòng)
Các chuỗi được kiểm tra
Ví dụ
4 1031204 21104 301041204 4120114 101101
Đầu ra
Yes/No
Ví dụ
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
#include <math.h>
int row = 0;
struct node{
int data;
struct node* next;
char edgetype;
}typedef node;
// Adds an edge to an adjacency list
node* push(node* first , char edgetype , int data){
node* new_node = (node*)malloc(sizeof(node));
new_node->edgetype = edgetype;
new_node->data = data;
new_node->next = NULL;
if (first==NULL){
first = new_node;
return new_node;
}
first->next = push(first->next,edgetype,data);
return first;
}
//Recursive function to check acceptance of input
int nfa(node** graph, int current, char* input,
int* accept, int start){
if (start==(int)strlen(input))
return accept[current];
node* temp = graph[current];
while (temp != NULL){
if (input[start]==temp->edgetype) {
if (nfa(graph,temp->data,input,accept,start+1==1)){
return 1;
}
}
temp=temp->next;
}
return 0;
}
//Function to generate binary strings of size n
void generate(char** arr, int size, char *a){
if (size==0){
strcpy(arr[row], a);
row++;
return;
}
char b0[20] = {'\0'};
char b1[20] = {'\0'};
b0[0] = '0';
b1[0] = '1';
generate((char**)arr, size-1, strcat(b0,a)); //Add 0 in front
generate((char**)arr, size-1, strcat(b1,a)); //Add 1 in front
return;
}
int main(){
int n;
int i, j;
scanf("%d", &n); //Number of nodes
node* graph[n+1]; //Create a graph
for (i=0;i<n+1;i++)
graph[i]=NULL;
int accept[n+1]; //Array to store state of vertex
for (i=0; i<n; i++){
//Index of vertex , Acceptance state , Number of edges
int index,acc,number_nodes;
scanf("%d%d%d",&index,&acc,&number_nodes);
accept[index]=acc; //Store acceptance
for (j=0;j<number_nodes;j++) //Add all edges{
int node_add;
int edge;
scanf("%d%d",&edge,&node_add);
graph[index] = push(graph[index],'0'+edge,node_add);
}
}
int size = 1; //Size of input
int count = 0; //Keep count of output strings
if (accept[1]==1) //Check for empty string{
printf("e\n");
count++;
}
while (count < 11){
char** arr;
int power = pow(2,size);
arr = (char**)malloc(power*sizeof(char*));
for (i=0;i<power;i++)
arr[i] = (char*)malloc(size*sizeof(char));
char a[20] = {'\0'};
generate((char**)arr,size,a); //Generate inputs
for (i=0; i<power; i++){
char input[20] = {'\0'};
for (j=0; j<size; j++){
char foo[2];
foo[0] = arr[i][size-1-j];
foo[1] = '\0';
strcat(input,foo);
//Copy generated string input
}
int result = nfa(graph,1,input,accept,0);
// Store result of nfa
if (result==1){
printf("%s\n",input);
count++;
}
if (count==10)
return 0;
}
size++; //Increment size of binary string input
row=0;
}
return 0;
} Đầu vào
4 1 0 4 0 1 0 2 1 1 1 3 2 0 1 0 4 3 0 1 1 4 4 1 2 0 4 1 4
Đầu ra
00 11 000 001 011 100 110 111 0000 0001
